This chapter focuses on compositional data analysis (CoDA). It is organized this way: First, we describe overall compositional data, the reasons that microbiome data can be treated as compositional, Aitchison simplex, challenges of analysis of compositional data, some fundamental principles of CoDA, and the family of log-ratio transformations (Sect. 14.1). Then, we introduce three methods or models of CoDA: ANOVA-like compositional differential abundance analysis (ALDEx2) (Sect. 14.2), analysis of composition of microbiomes (ANCOM) (Sect. 14.3), and analysis of composition of microbiomes-bias correction (ANCOM-BC) (Sect. 14.4). Next, we make some remarks on CoDA approach (Sect. 14.5). Finally, we complete this chapter with a brief summary of CoDA in Sect. 14.6.
14.1 Introduction to Compositional Data
14.1.1 What Are Compositional Data?
Composition is “the act of putting together parts or elements to form a whole” and is “the way in which such parts are combined or related: constitution” (Webster’s II New College Dictionary, 2005, p.236) [also see (Xia et al. 2018a)]. As described in Aitchison’s 1986 seminar work (Aitchison 1986b), a compositional dataset has the following four characteristics: (1) each row presents an observational unit; (2) each column presents an composition of whole; (3) each entry is non-negative; and (4) the sum of all the entries in each row equals to 1 or 100%. That is, compositional data quantitatively measure each element as a composition or describe the parts of the whole, a vector of non-zero positive values (i.e., components or parts) carrying only relative information between their components or parts (Pawlowsky-Glahn et al. 2015; Hron et al. 2010; Egozcue and Pawlowsky-Glahn 2011; Aitchison 1986a). Thus, compositional data exist as the proportions/fractions of a whole or the portions of a total (van den Boogaart and Tolosana-Delgado 2013a) and have the following unique properties: (1) The elements of the composition are non-negative and sum to unity (Bacon-Shone 2011; Xia et al. 2018a). (2) The total sum of all component values (i.e., the library size) is an artifact of the sampling procedure (Quinn et al. 2018a, b; van den Boogaart and Tolosana-Delgado 2008). (3) The difference between component values is only meaningful proportionally (Quinn et al. 2018a, b; van den Boogaart and Tolosana-Delgado 2008). The unique properties, especially adding up all the percentages of compositions necessarily to 100, introduces effects on correlations (Krumbein 1962).
14.1.2 Microbiome Data Are Treated as Compositional
Compositional data analysis is really only interested in relative frequencies rather than the absolute amount of data. Thus, compositional data analysis frequently arises in various research fields, including genomics, population genetics, demography, ecology, biology, chemistry, geology, petrology, sedimentology, geochemistry, planetology, psychology, marketing, survey analysis, economics, probability, and statistics.
- (1)
The high-throughput sequencing technology itself predefines or constrains the sequencing data including microbiome data to some constants (each sample read counts are constrained by an arbitrary total sum, i.e., library size) when sequencing platforms were used to generate the data (Quinn et al. 2018a, b), resulting in the total values of the data meaningless. Regardless the datasets are generated via 16S rRNA gene fragments sequencing or shotgun metagenomic sequencing, the observed number of reads (sequencing depth) is determined by the capacity of the sequencing platform used and the number of samples that are multiplexed in the run (Fernandes et al. 2014). Thus, the total reads mapped from the high-throughput sequencing methods are finite although they are large.
- (2)
Sample preparation and DNA/RNA extraction process cause each entry of microbiome datasets to carry only relative information in the measurements of feature (OTU or taxa abundance) (Lovell et al. 2011). RNA sequencing begins with extraction of the tissue of DNA/RNA samples. However, the tissue weight or volume is fixed. Thus, the number of sequence fragment reads obtained from a fixed volumes of total RNA is finite.
- (3)
In practice, to reduce experimental biases due to sampling depth and the biases of sample preparation and DNA/RNA extraction, the abundance read counts are typically divided by the total sum of counts in the sample(total library sizes) to normalize the data before analysis. All these result in microbiome dataset having compositional data structure and the abundance of each component (e.g., taxon/OTU) carries only relative information and hence is only coherently interpretable relative to other components within that sample (Quinn et al. 2018a, b).
14.1.3 Aitchison Simplex
Mathematically, a data is defined as compositional, if it contains D multiple parts of nonnegative numbers whose sum is 1 (Aitchison 1986a, p. 25) or any constant-sum constraint (Pawlowsky-Glahn et al. 2015, p. 10). It can be formally stated as:
![$$ {S}^D=\left\{X=\left[{x}_1,{x}_2,\dots, {x}_D\right]\left|{x}_i>0,i=1,2,\dots, D;\sum \limits_{i=1}^D{x}_i=\kappa \right.\right\}. $$](images/486056_1_En_14_Chapter_TeX_Equ1.png)
That is, compositional data can be represented by constant sum real vectors with positive components. Where 𝜅 is arbitrary. Depending on the units of measurement or rescaling, frequent values are 1 (per unit, proportions), 100 (percent, %), (ppm, parts per million), and (ppb, parts per billion). The equation of 14.1 defines the sample space of compositional data as a hyperplane, called the simplex (Aitchison 1986a, p. 27). Also see (Mateu-Figueras et al. 2011; van den Boogaart and Tolosana-Delgado 2013a, p. 37) and (Pawlowsky-Glahn et al. 2015, p. 10). Compositional data do not exist in real Euclidean space, but rather in the simplex (a sub-space) (Aitchison 1986a).
14.1.4 Challenges of Analyzing Compositional Data
Standard methods (e.g., correlation analysis) rely on the assumption of Euclidean geometry in real space (i.e., P) (Eaton 1983) and assume that the differences between the tested variables are linear or additive. However, the simplex has one dimension less than real space (i.e., P-1), which represent special properties of the sample space (Aitchison 1986a). Therefore, in compositional data each component (or part) of the whole is dependent on other components. Because the sum of all proportions of each component equals to 1 (100%), at least two components are negatively correlated. This results in the dependency problem of the measured variables (e.g., taxa/OTUs/ASVs). In the statistical and especially in current microbiome literatures, the issue of dealing with proportions is referred as to compositionality. Microbial abundances are typically interpreted as proportions (e.g., relative abundance) to account for differences in sequencing depth (see Sect. 14.1.2 for details). Because proportions add to one, the change of a single microbial taxon will also change the proportions of the remaining microbial taxa. Therefore, it poses a challenge to infer exactly which microbial taxon is changing with treatments or conditions.
It was shown that two-sample t-tests and Wilcoxon rank sum tests have a higher FDR and low power to detect differential abundance because of ignoring the compositionality or dependency effect (microbial taxa in the same niche grow dependently) (Hawinkel et al. 2017).
Analyzing compositional (or relative) data using Pearson and Spearman correlations will lead to the problem of “spurious correlation” between unrelated variables (Pearson 1897). Compositional data are not linear or monotonic; instead they exhibit dependence between components. Pearson and Spearman correlation analysis methods were originally proposed for absolute values. The dependence of each pair of components of compositional data violates the assumption that the paired data are randomly selected (independent) by linear (i.e., for Pearson) or rank (i.e., for Spearman) correlation.
Visualizing or presenting compositional data using standard graphical tools (e.g., scatter plot, QQ plot) will result in a distorted graph.
Analyzing compositional data using multivariate parametric models (e.g., MANOVA) violates the assumption of multivariate parametric analysis. Standard multivariate parametric models, such as MANOVA and multivariate linear regression, assume that the response variables are multivariate and normally distributed and have a linear relationship between response variables and predictors. However, compositional data are not multivariate normally distributed. Thus, using MANOVA (or ANOVA) and multivariate (or univariate) linear regression to test hypotheses on the response variable is meaningless due to dependence of the compositions.
14.1.5 Fundamental Principles of Compositional Data Analysis
Aitchison proposed and suggested (Aitchison 1982, 1986a) three fundamental principles for the analysis of compositional data that we should adhere to when analyzing compositional data. These fundamental principles are all rooted in the definition of compositional data: only ratios of components carry information and have been reformulated several times according to new theoretical developments (Barceló-Vidal et al. 2001; Martín-Fernández et al. 2003; Aitchison and Egozcue 2005; Egozcue 2009; Egozcue and Pawlowsky-Glahn 2011). The three fundamental principles are: (1) scaling invariance; (2) subcompositional coherence; and (3) permutation invariance.
In 2008, Aitchison summarized basic principle of compositional data analysis. For its formal expression, we cannot do better than to quote his definition (Aitchison 2008):
Any meaningful function of a composition can be expressed in terms of ratios of the components of the composition. Perhaps equally important is that any function of a composition not expressible in terms of ratios of the components is meaningless.
Scaling invariance states that vectors with proportional positive components must be treated (analyzed) as representing the same composition (Lovell et al. 2015). That is, statistical inferences about compositional data should not depend on the scale used; i.e., a composition is multiplied by a constant k will not change the results (van den Boogaart and Tolosana-Delgado 2013b). Thus, the vector of per-units and the vector of percentages convey exactly the same information (Egozcue and Pawlowsky-Glahn 2011). We should obtain exactly the same results from analyzing proportions and percentages. For example, the vectors a = [11, 2, 5], b = [110, 20, 50], and c = [1100, 200, 500] represent all the same composition because the relative importance (the ratios) between their components is the same (van den Boogaart and Tolosana-Delgado 2013b).
Subcompositional coherence states that analyses should depend only on data about components (or parts) within that subset, not depend on other non-involved components (or parts) (Egozcue and Pawlowsky-Glahn 2011); and statistical inferences about subcompositions (a particular subset of components) should be consistent, regardless of whether the inference is based on the subcomposition or the full composition (Lovell et al. 2015).
Permutation invariance states that the conclusions of a compositional analysis should not depend on the order (the sequence) of the components (the parts) (Egozcue and Pawlowsky-Glahn 2011; van den Boogaart and Tolosana-Delgado 2013b; Lovell et al. 2015). That is, in compositional analysis, the information from the order of the different components plays no role (i.e., changing the order of the components within a composition will not change the results) (van den Boogaart and Tolosana-Delgado 2013b; Quinn et al. 2018a, b). For example, it does not matter that we choose which component to be the “first,” which component to be the “second,” and which one to be the “last.”
Other important properties of CoDa include perturbation invariance and subcompositional dominance. Perturbation invariance states that converting a composition between equivalent units will not change the results (van den Boogaart and Tolosana-Delgado 2013b; Quinn et al. 2018a, b).
Subcompositional dominance states that using a subset of a complete composition carries less information than using the whole (van den Boogaart and Tolosana-Delgado 2013b; Quinn et al. 2018a, b).
14.1.6 The Family of Log-Ratio Transformations
Compositional data exist in the Aitchison simplex (Aitchison 1986a), while the most statistical methods or models are valid in Euclidean space (real space). Aitchison (1981, 1982, 1983, 1984, 1986a; Aitchison and Egozcue 2005) approved that compositional data could be mapped into Euclidean space by using the log-ratio transformation and then can be analyzed using standard statistical methods or models such as an Euclidean distance metric (Aitchison et al. 2000). Thus, usually most compositional data analyses start with a log-ratio transformation (Xia et al. 2018a).
The algorithm behind the log-ratio transformation principle is that compositional vectors and associated log-ratio vectors exist a one-to-one correspondence so that any statement about compositions can be reformed in terms of log-ratios and vice versa (Pawlowsky-Glahn et al. 2015). Thus, log-ratio transformations solve the problem of a constrained sample space by projecting compositional data in the simplex into multivariate real space. Therefore, open up all available standard multivariate techniques (Pawlowsky-Glahn et al. 2015).
In order to transform the simplex to the real space, Aitchison in his seminal work (1986a, b) developed a set of fundamental principles, a variety of methods, operations, and tools, including the additive log-ratio (alr) for compositional data analysis.
The log-ratio transformation methodology has been accepted in various fields such as geology and ecology (Pawlowsky-Glahn and Buccianti 2011; van den Boogaart and Tolosana-Delgado 2013a; Aitchison 1982; Pawlowsky-Glahn et al. 2015). Here, we introduce the family of log-ratio transformations including the additive log-ratio (alr) (Aitchison 1986a, p. 135), the centered log-ratio (clr) (Aitchison 2003), the inter-quartile log-ratio (iqlr) (Fernandes et al. 2013, 2014), and isometric log-ratio (ilr) (Egozcue et al. 2003) transformations.
14.1.6.1 Additive Log-Ratio (alr) Transformation
The original approach of compositional data analysis proposed in Aitchison (1986a, b) was based on the alr-transformation. It is defined as:
![$$ \mathrm{alr}(x)=\left[\ln \left(\frac{x_1}{x_D}\right),\dots, \ln \left(\frac{x_i}{x_D}\right),\dots, \ln \left(\frac{x_{D-1}}{x_D}\right)\right]. $$](images/486056_1_En_14_Chapter_TeX_Equ2.png)
This formula maps a composition in the D-part Aitchison simplex none isometrically to a D-1 dimensional Euclidean vector. The alr-transformation chooses one component as a reference and takes the logarithm of each measurement within a composition vector (i.e., in the microbiome case, each sample vector containing relative abundances) after divided by a reference taxon (usually the taxon with index D, with D being the total number of taxon is chosen). Sum of all Xj to unity, but we can replace the components with any observed counts, which do not change the expression due to the library sizes cancelation. After the alr-transformation, any separation between the groups revealed by the ratios can be analyzed by standard statistical tools (Thomas and Aitchison 2006).
14.1.6.2 Centered Log-Ratio (clr) Transformation
The clr-transformation is defined as the logarithm of the components after dividing by the geometric mean of x:
![$$ clr(x)=\left[\ln \left(\frac{x_1}{g_m(x)}\right),\dots, \ln \left(\frac{x_i}{g_m(x)}\right),\dots, \ln \left(\frac{x_D}{g_m(x)}\right)\right], $$](images/486056_1_En_14_Chapter_TeX_Equ3.png)
with ![$$ {g}_m(x)=\sqrt[D]{x_1\cdot {x}_2\cdots {x}_D} $$](images/486056_1_En_14_Chapter_TeX_IEq1.png) ensuring that the sum of the elements of clr(x) is zero. Where x = (x1, …, xi, …, xD) represents the composition. The clr-transformation maps a composition in the D-part Aitchison simplex isometrically to a D-1 dimensional Euclidean vector. Unlike the alr-transformation in which a specific taxon is used as reference, the clr-transformation uses the geometric mean of the composition (i.e., sample vector) in place of xD. Like the alr, after performing the clr-transformation, the standard unconstrained statistical methods can be used for analyzing compositional data (Aitchison 2003).
ensuring that the sum of the elements of clr(x) is zero. Where x = (x1, …, xi, …, xD) represents the composition. The clr-transformation maps a composition in the D-part Aitchison simplex isometrically to a D-1 dimensional Euclidean vector. Unlike the alr-transformation in which a specific taxon is used as reference, the clr-transformation uses the geometric mean of the composition (i.e., sample vector) in place of xD. Like the alr, after performing the clr-transformation, the standard unconstrained statistical methods can be used for analyzing compositional data (Aitchison 2003).
The clr-transformation algorithm has been adopted by some software (van den Boogaart and Tolosana-Delgado 2013b; Fernandes et al. 2013), and it was shown it could be used to analyze microbiome data and RNA-seq data and other next-generation sequencing data (Fernandes et al. 2014).
14.1.6.3 Isometric Log-Ratio (ilr) Transformation
The ilr-transformation is defined as:

![$$ {y}_i=\frac{1}{\sqrt{i\left(i+1\right)}}\ln \left[\frac{\Pi_{j=1}^i{x}_j}{\left({x}_i+1\right)i}\right]. $$](images/486056_1_En_14_Chapter_TeX_IEq2.png)
Like the clr, the ilr-transformation maps a composition in the D-part Aitchison simplex isometrically to a D-1 dimensional Euclidian vector. This ilr-transformation is an orthonormal isometry. It is the product of the clr and the transpose of a matrix which consists of elements. The elements are clr-transformed components of an orthonormal basis. The ilr-transformation transforms the data regarding an orthonormal coordinate system that performed from sequential binary partitions of taxa (van den Boogaart and Tolosana-Delgado 2013b).
Like alr and clr, ilr-transformation was developed to transform compositional data from the simplex into real space where standard statistical tools can be applied (Egozcue and Pawlowsky-Glahn 2005; Egozcue et al. 2003). That is, the ilr-transformed data can be analyzed using the standard statistical methods.
14.1.6.4 Inter-quartile Log-Ratio (iqlr) Transformation
The inter-quartile log-ratio (iqlr) transformation introduced in the ALDEx2 package (Fernandes et al. 2013, 2014) is defined as including only taxa that fall within the inter-quartile range of total variance in the geometric mean calculation. That is, the iqlr-transformation uses the geometric mean of a taxon subset as the reference.
14.1.7 Remarks on Log-Ratio Transformations
- (1)
alr-transformation
- The strengths of alr-transformation are:
It is the simplest transformation in the log-ratio transformation family and hence is relatively simple to interpret the results.
The relation to the original D-1 first parts is preserved and it is still in wide use.
- The weaknesses of alr-transformation are:
It is not an isometric transformation from the Aitchison simplex metric into the real alr-space with the ordinary Euclidean metric. Although this weakness could be solved using an appropriate metric with oblique coordinates in real additive log-ratio (alr) space. However, it is not a standard practice (Aitchison and Egozcue 2005).
Theoretically, we cannot use the standard statistical methods such as ANOVA and t-test to analyze the alr-transformed data. Although this weakness is a conceptual rather than practical problem (Aitchison et al. 2000) and this transformation was used in Aitchison (1986a, b) and further developed in Aitchison et al. (2000), by definition, the alr-transformation is asymmetric in the parts of the composition (Egozcue et al. 2003); thus, the distances between points in the transformed space are not the same for different divisors (Bacon-Shone 2011).
The practical problem is not always easy to choose an obvious reference and the choice of reference taxon is somewhat arbitrary (Li 2015), and results may vary substantially when the difference references are chosen (Tsilimigras and Fodor 2016). This may explain that the alr-transformation was an optional transformation approach but not default approach in Analyzing Compositional Data with R (van den Boogaart and Tolosana-Delgado 2013a, b).
- (2)
clr-transformation
- The strengths of clr-transformation are:
It avoids the alr-transformation problem of choosing a divisor (e.g., using one reference taxon) because the clr-transformation uses the geometric mean as the divisor.
It is an isometric transformation of the simplex with the Aitchison metric, onto a subspace of real space with the ordinary Euclidean metric (Egozcue et al. 2003).
Thus, it is most often used transformation in literature of compositional data analysis (CoDA) (Xia et al. 2018a).
- The weaknesses of clr-transformation are:
- (3)
ilr-transformation
- The strengths of ilr-transformation are:
It has significant conceptual advantages (Bacon-Shone 2011).
It avoids the arbitrariness of alr and the singularity of clr; thus, it addresses certain difficulties of alr and clr and the ilr-transformed data can be analyzed using all the standard statistical methods.
- However, the ilr-transformation has the weaknesses and been criticized because of the following difficulties:
It has a major difficulty to naturally model the practical compositional situations in terms of a sequence of orthogonal logcontrasts, which is in contrast to the practical use of othogonality when using the simplicial singular value decomposition (Aitchison 2008). In other words, the ilr-transformation approach violates the practical use of the principal component analysis or principal logcontrast analysis in CoDA (Aitchison 1983, 1986a).
Ensuring isometry has little to do with this compositional problem, and actually the coordinates in any ilr-transformation necessarily require a set of orthogonal logcontrasts, which in clinical practice lacks of interpretability (Aitchison 2008) or its interpretability is dependent on the selection of its basis (Egozcue et al. 2003).
There is no one-to-one relation between the original components and the transformed variables.
Due to these limitations and specifically the difficulty to interpret the results. In practice, ilr has somewhat limited its adoption or application (Egozcue et al. 2003; Xia et al. 2018a).
- (4)
iqlr-transformation
Compared to other three log-ratio transformations, the iqlr-transformation is not getting widely applied.
14.2 ANOVA-Like Compositional Differential Abundance Analysis
Previously, most existing tools for compositional data analysis have been used in the other fields, such as geology and ecology. ANOVA-Like Differential Expression (ALDEx) analysis is one of early statistical methods that were developed under a framework of compositional analysis for mixed population RNA-seq experiment.
14.2.1 Introduction to ALDEx2
ALDEx (Fernandes et al. 2013) and ALDEx2 (Fernandes et al. 2014) were initially developed for analyzing differential expression of mixed population RNA sequencing (RNA-seq) data, but it has been showed that this approach is essentially generalizable to nearly any type of high-throughput sequencing data, including three completely different experimental designs: the traditional RNA-seq, 16S rRNA gene amplicon-sequencing, and selective growth-type (SELEX) experiments (Fernandes et al. 2014; Gloor and Reid 2016; Gloor et al. 2016; Urbaniak et al. 2016). The R packages called ALDEx and ALDEx2 have been used to analyze unified high-throughput sequencing datasets such as RNA-seq, chromatin immunoprecipitation sequencing (ChIP-seq), 16S rRNA gene sequencing fragments, metagenomic sequencing, and selective growth experiments (Fernandes et al. 2014).
High-throughput sequencing (e.g., microbiome) data have several sources of variance including sampling replication, technical replication, variability within biological conditions, and variability between biological conditions. ALDEx and ALDEx2 were developed in a traditional ANOVA-like framework that decompose sample-to-sample variation into four parts: (1) within-condition variation, (2) between-condition variation, (3) sampling variation, and (4) general (unexplained) error.
Fernandes et al. (2013) highlighted the importance for partitioning and comparing biological between-condition and within-condition differences (variation), and hence they developed ALDEx, an ANOVA-like differential expression procedure, to identify genes (in the case, taxa/OTUs) with greater between- to within-condition differences via the parametric Welch’s t-test or a non-parametric testing such as Wilcoxon rank sum test or Kruskal-Wallis test (Fernandes et al. 2013, 2014).
ALDEx was developed using the equivalency between Poisson and multinomial processes to infer proportions from counts and model the data as “compositional” or “proportional.” In other words, ALDEx2 uses log-ratio transformation rather than effective library size normalization in count-based differential expression studies. However, when sample sizes are small, the marginal proportions have the large variance and extremely not normally distributed. Thus, ALDEx performs all inferences based on the compositionally valid Dirichlet distribution, i.e., using the full posterior distribution of probabilities drawn from the Dirichlet distribution through Bayesian techniques.
Part 1: Convert the observed abundances into relative abundances by Monte Carlo (MC) sampling.
Like other CoDa approaches, ALDEx is not interested in the total number of reads, instead of inferring proportions from counts. Denote ni present the number of counts observed in taxon i, and assume that each taxon’s read count was sampled from a Poisson process with rate μi, i.e., ni~Poisson(μi) with n = ∑ini. Then, the set of joint counts with given total read counts has a multinomial distribution, i.e., {[n1, n2, …]| n} ~ Multinomial (p1, p2, …| n) where each pi = μi/∑kμk based on the equivalency between Poisson and multinomial processes.
Since the Poisson process is equivalent to the multinomial process, traditional methods use ni to estimate μi and then use the set of μi to estimate pi. These methods ignore that most datasets of this type contain large numbers of taxa with zero or small read counts; thus the maximum-likelihood estimate of pi this way is often exponentially inaccurate. Therefore, ALDEx estimate the set of proportions pi directly from the set of counts ni. ALDEx uses standard Bayesian techniques to infer the posterior distribution of [p1, p2, …] as the product of the multinomial likelihood with a Dirichlet ( ,
, 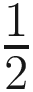 ,…) prior. Considering the large variance and extreme non-normality of the marginal distributions pi when the associated ni are small, ALDEx does not summarize the posterior of pi using point-estimates. Instead, it performs all inferences using the full posterior distribution of probabilities drawn from the Dirichlet distribution such that [pi, p2, …]~ Dirichlet
,…) prior. Considering the large variance and extreme non-normality of the marginal distributions pi when the associated ni are small, ALDEx does not summarize the posterior of pi using point-estimates. Instead, it performs all inferences using the full posterior distribution of probabilities drawn from the Dirichlet distribution such that [pi, p2, …]~ Dirichlet ![$$ \left(\left[{n}_1,{n}_2,\dots \right]+\frac{1}{2}\right) $$](images/486056_1_En_14_Chapter_TeX_IEq5.png) . Adding 0.5 to the Dirichlet distribution, the multivariate distribution avoids the zero problem for the inferred proportions even if the associated count is zero and conserves the probability, i.e., ∑kpk = 1.
. Adding 0.5 to the Dirichlet distribution, the multivariate distribution avoids the zero problem for the inferred proportions even if the associated count is zero and conserves the probability, i.e., ∑kpk = 1.
Because mathematically log-proportions are easily manipulated, ALDEx takes the component-wise logarithms and subtracts the constant 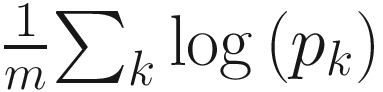 from each log-proportion component for a set of m proportions [pi, p2, …, pm]. This results in the values of the relative abundances
from each log-proportion component for a set of m proportions [pi, p2, …, pm]. This results in the values of the relative abundances 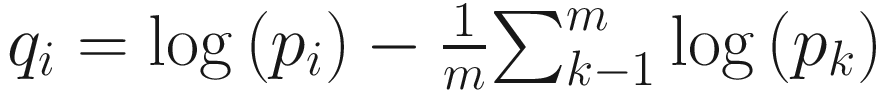 where ∑kqk is always zero. Most important, it projects q onto a m − 1 dimensional Euclidean vector space with linearly independent components. Thus, a traditional ANOVA-like framework can be formed to analyze the q values [qi, q2, …, qm].
where ∑kqk is always zero. Most important, it projects q onto a m − 1 dimensional Euclidean vector space with linearly independent components. Thus, a traditional ANOVA-like framework can be formed to analyze the q values [qi, q2, …, qm].
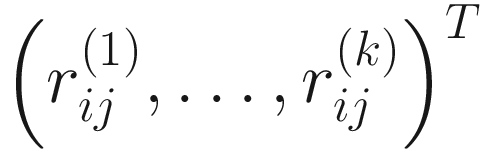 . This renders the data free of zeros.
. This renders the data free of zeros.Part 2: Perform log-ratio transformation on each of the so-called Monte Carlo (MC) instances usually most through clr- or iqlr-transformation
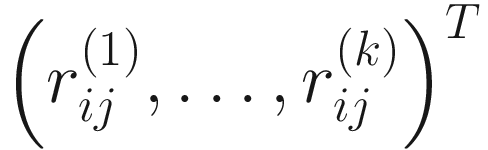 for each sample j and each MC Dirichlet realization k, k = 1, …, K. The distributions are estimated from multiple independent Monte Carlo realizations of their underlying Dirichlet-distributed proportions for all taxa (genes) i simultaneously.
for each sample j and each MC Dirichlet realization k, k = 1, …, K. The distributions are estimated from multiple independent Monte Carlo realizations of their underlying Dirichlet-distributed proportions for all taxa (genes) i simultaneously.Part 3: Perform statistical hypothesis testing on each MC instance, i.e., each taxon in the vector of clr or iqlr transformed values, to generate P-values (P) for each transcript
The hypothesis testing is performed using the classical statistical tests, i.e., Welch’s t and Wilcoxon rank sum tests for two groups, and glm and Kruskal-Wallis for two or more groups. Since there is a total of K MC Dirichlet samples, each taxon will have K P-values.
Let i = {1, 2, …, I} index taxa (genes), j = {1, 2, …, J} index the groups (conditions), and k = {1, 2, …, Kj} index the replicate of a given group(condition), using the framework of random-effect ANOVA models, the ALDEx model is given as below.
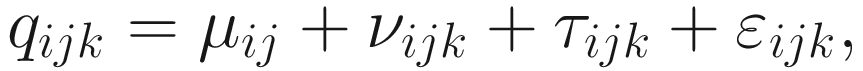
Here, νijk is assumed to be approximately normal as in the usual ANOVA models. The sampling error τijk is given by the adjusted log-marginal distributions of the Dirichlet posterior and its distribution is very Gaussian-like. To ensure it is more appropriate for the analysis of high-throughput sequencing datasets, ALDEx does not assume that within-group (condition) sample-to-sample variation is small and essentially negligible.
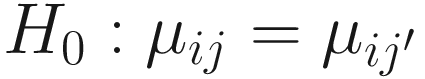
Part 4: Average these P-values across all MC instances to yield expected P-values for each taxon.
The expected P-values are Benjamini-Hochberg adjusted P-values (BH) by using Benjamini-Hochberg correction procedure (Benjamini and Hochberg 1995).
Part 5: Develop an estimated effect size metric to compare the predicted between-group differences to within-group differences.
The authors of this model (Fernandes et al. 2013) emphasize the statistical significance by this hypothesis testing in Part 3 above does not imply that the groups (conditions) j and j′ are meaningfully different. Instead, such meaning can be inferred through an estimated effect size that compares predicted between group (condition) differences to within-group(condition) differences.
Given the set of random variables pijk and qijk, the within-group (condition) distribution is:
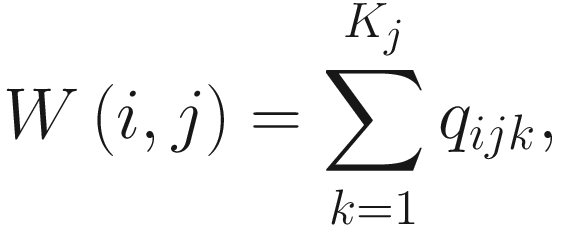
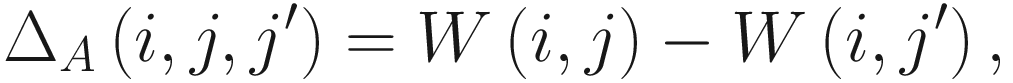
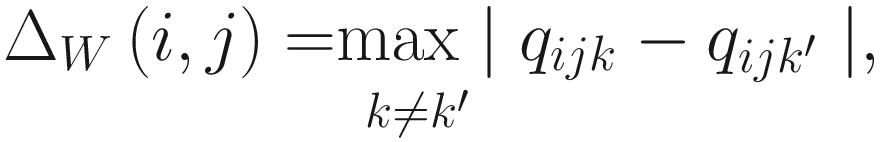
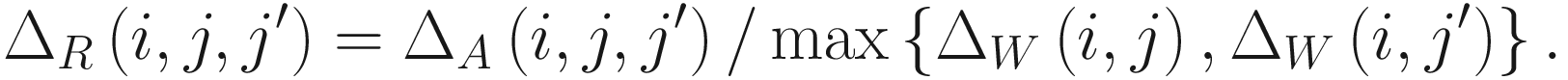
The effect size metric in ALDEx2 is another statistical method that was developed specifically for this package and is recommended for use over the P-values.
For normally distributed data, usually effect sizes measure the standardized mean difference between groups, such as Cohen’s d (1988) measures the standardized difference between two means. Cohen’s d has been widely used in behavioral sciences accompanying reporting of t-test and ANOVA results and meta-analysis. However, in high-throughput sequencing data, the data are often not normally distributed. For non-normality of data, it is very difficult to measure effect sizes and interpret them.
ALDEx2 effect size measure estimates the median standardized difference between groups. It is a standardized distributional effect size metric. To obtain this effect size, take the median of differences (about -2), which provides a non-parametric measure of the between-group difference. Then, scale (normalize) the median of differences by the dispersion: effect = median (difference / dispersion). Where dispersion = maximum (vector a-randomly permutated vector a, vector b- randomly permutated vector b). In the aldex.effect module output, these measures are denoted as: diff.btw = median(diff), diff.win = median(disp), and effect = eff. ALDEx2 also provides a 95% confidence interval of the effect size estimate if in the aldex.effect() function, CI=TRUE is specified (see Sect. 14.2.2).
It was shown that ALDEx2 effect size is somewhat robust and is approximately 1.4 times that of Cohen’s d, as expected for a well-behaved non-parametric estimator. It is equally valid for normal, random uniform, and Cauchy distributions (Fernandes et al. 2018).
14.2.2 Implement ALDEx2 Using R
ALDEx2 takes the compositional data analysis approach that uses Bayesian methods to infer technical and statistical error (Fernandes et al. 2014). ALDEx2 incorporates a Bayesian estimate of the posterior probability of taxon abundance into a compositional framework; that is, it uses a Dirichlet distribution to transform the observed data and then estimates the distribution of taxon abundance by random sampling instances of the transformed data. There are two essential procedures: ALDEx2 first takes the original input data and generates a distribution of posterior probabilities of observing each taxon; then it uses the centered log-ratio transformation to transform this distribution. After centered log-ratio transforming the distribution, a parametric or nonparametric t-test or ANOVA can be performed for the univariate statistical tests and the P-values and Benjamini-Hochberg adjusted P-values are returned.
The ALDEx2 methods are available from the ALDEx2 package (current version 1.27.0, October 2021). There are three approaches that can be used to implement ALDEx2 methods: (1) Bioconductor ALDEx2 modular, (2) ALDEx2 wrapper, and (3) the aldex.glm module. Bioconductor version of ALDEx2 is modular, which is achieved by exposing the underlying center log-ratio transformed Dirichlet Monte-Carlo replicate values and hence is flexible for adding the specific R commands by the users based on their experimental design. Thus, it is suitable for the comparison of many different experimental designs. Currently, the ALDEx2 wrapper is limited to a two-sample t-test (and calculation of effect sizes) and one-way ANOVA design. The aldex.glm module was developed to implement the probabilistic compositional approach for complex study designs.
We illustrated this package in our previous book (Xia et al. 2018a). In this section, we illustrate these three approaches in turn with a new microbiome dataset.
This example dataset was introduced in Chap. 9 (Example 9.1). In this dataset, the mouse fecal samples were collected at two time points: pre-treatment and post-treatment. Here we are interested in comparison of the microbiome difference between Genotype (breast cancer cell lines MCF-7 cell (WT) and MCF-7 knockout) at post-treatment.
There are two ways to install the ALDEx2 package. The most recent version of ALDEx2 is available from github.com/ggloor/ALDEx_bioc. It is recommended to run the most up-to-date R and Bioconductor version of ALDEx2. Here we install this stable version of ALDEx2 from Bioconductor.
The aldex modular offers the users to specify their own tests, and then the ALDEx2 modular exposes the underlying intermediate data. To simplify, the ALDEx2 modular approach is just to call aldex.clr, aldex.ttest, and aldex.effect modules (functions) in turn and then merge the data into one data frame. We use the following seven steps to perform ALDEx2 by using the modular approach.
Step 1: Load OTU-table and sample metadata.
Step 2: Run the aldex.clr module to generate the random centered log-ratio transformed values.
counts table(OTU abundance table), a vector of groups, and the number of Monte-Carlo are the three required inputs.
denom is used to specify a string for indicating if iqlr, zero, or all features are used as the denominator.
verbosity is used to specify the level of verbosity (TRUE or FALSE).
Step 3: Run the aldex.ttest module to perform the Welch’s t and Wilcoxon rank sum test.
aldex_clr is the aldex object from aldex.clr module.
paired.test is used to specify whether a paired test should be conducted or not (TRUE or FALSE).
The aldex.ttest() returns the values of we.ep (expected P-value of Welch’s t test), we.eBH (expected Benjamini-Hochberg corrected P-value of Welch’s t test), wi.ep (expected P-value of Wilcoxon rank test), and wi.eBH (expected Benjamini-Hochberg corrected P-value of Wilcoxon test).
As an alternative method of the t-test, we can run the aldex.kw module to perform the Kruskal-Wallis and glm tests for one-way ANOVA, which compares two or more groups.
Step 4: Run the aldex.effect module to estimate effect size and the within and between group values.
aldex_clr is the aldex object from aldex.clr module.
CI is used to indicate whether to include the 95% confidence interval information for the effect size estimate (TRUE or FALSE).
verbose is used to specify the level of verbosity.
rab.all (median clr value for all samples in the feature).
rab.win.KO (median clr value for the KO group of samples).
rab.win.WT (median clr value for the WT group of samples).
dif.btw (median difference in clr values between KO and WT groups).
dif.win (median of the largest difference in clr values within KO and WT groups).
effect (median effect size: diff.btw / max(diff.win) and effect.low and effect.high for all instances.
overlap (proportion of effect size that overlaps between the Bayesian distribution of groups KO and WT; i.e., if the overlap is 0: no effect).
Step 5: Merge all data into one object and make a data frame for result viewing and downstream analysis.
Step 6: Run the aldex.plot module to generate the MA and MW (effect) plots.
Bland-Altman plot (difference plot, or Tukey mean-difference plot), named after J. Martin Bland and Douglas G. Altman, is a data plotting method for analyzing the agreement between two different measures (Altman and Bland 1983; Martin Bland and Altman 1986; Bland and Altman 1999). Bland-Altman method states that any two methods designing to measure the same property or parameter are not merely highly correlated but also should have agreed sufficiently closely. ALDEx2 provides a Bland-Altman (MA) style plot to graphically compare the degree of agreement of measures between median log2 between-condition difference and median log2 relative abundance.
Effect size in ALDEx2 is defined as a measure of the mean ratio of the difference between groups (diff.btw) and the maximum difference within groups (diff.win or variance). The effect size can be obtained by the aldex.effect modular or by specifying effect=TRUE argument using the aldex wrapper. The aldex.plot modular plots median between-group difference versus median within-group difference to visualize differential abundance of the sample data, which are referred to as “effect size” plots in ALDEx2.
The following commands generate the MA and MW (effect) plots (Fig. 14.1).
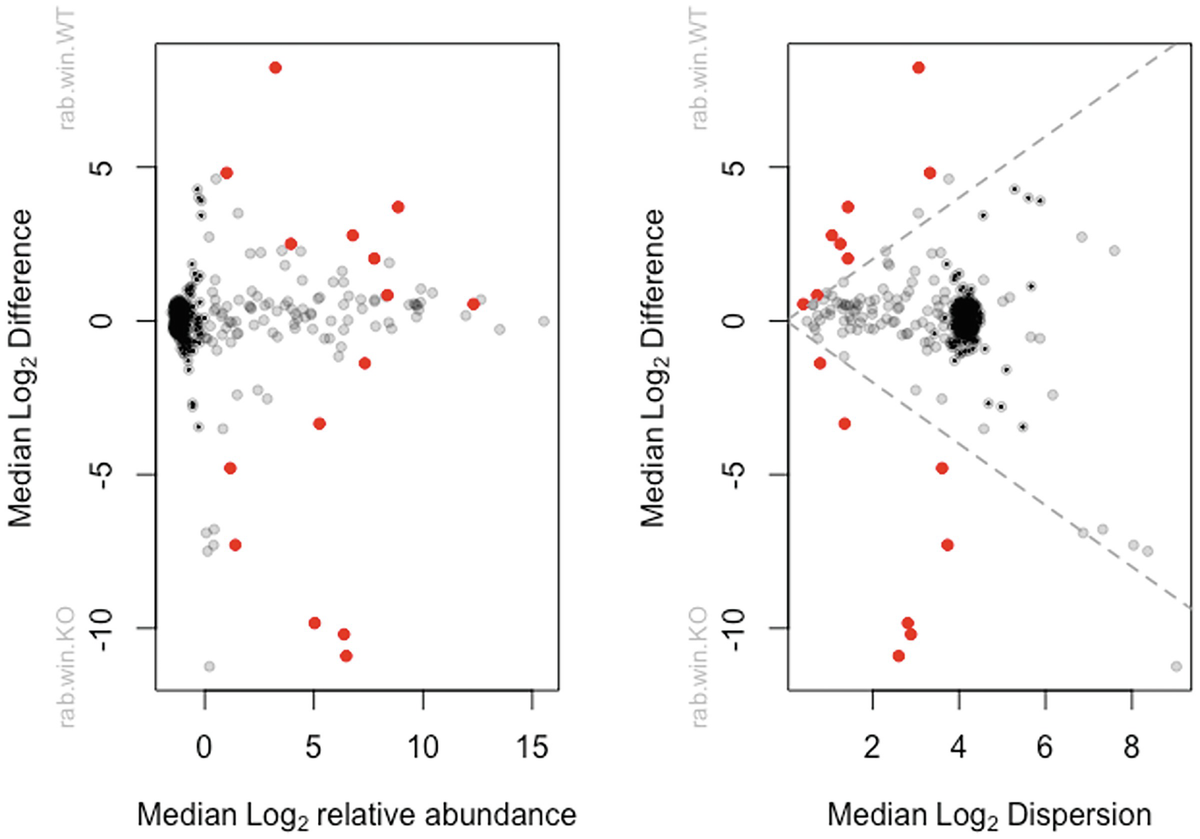
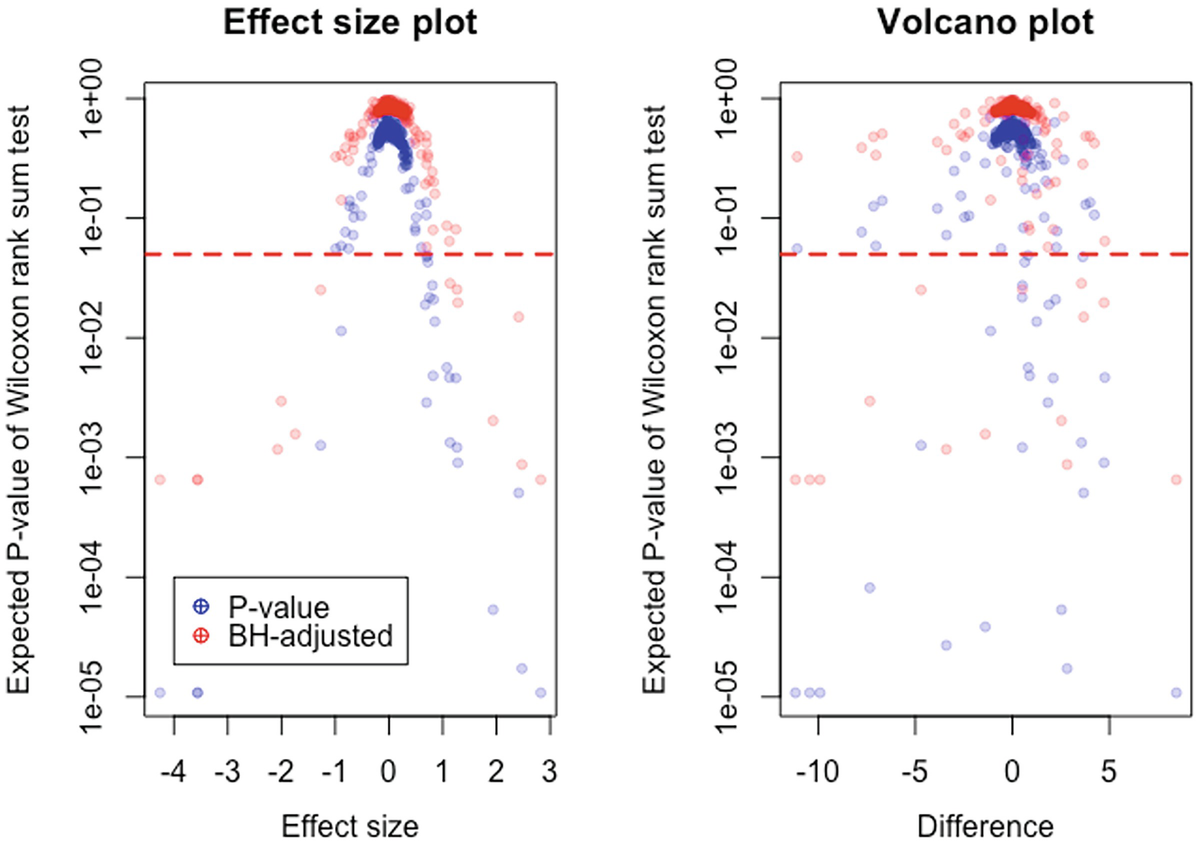
Two scatterplots of median log subscript 2 difference versus median log subscript 2 relative abundance and median log subscript 2 dispersion plot dots in red, gray, and black colors.
MA and MW (Effect) plots of ALDEx2 output from aldex.plot() function. The left panel is a Bland-Altman or MA plot that shows the relationship between (relative) abundance and difference. The right panel is an MW (effect) effect plot that shows the relationship between difference and dispersion. In both plots, red represents the statistically significant features that are differentially abundant with Q = 0.05; gray are abundant, but not differentially abundant; black are rare, but not differentially abundant. This function uses the combined output from the aldex.ttest () and aldex.effect() functions. The Log-ratio abundance axis is the clr value for the feature
ALDEx2 generates a posterior distribution of the probability of observing the count given the data collected. Importantly this approach generates the 95% CI of the effect size. ALDEx2 uses a standardized effect size, similar to the Cohen’s d metric. It was shown the effect size in ALDEx2 is more robust and more conservative (being approximately 0.7 Cohen’s d when the data are normally distributed based on Greg Gloor’s note in his AlDEx2_vignette of ANOVA-Like Differential Expression tool for high throughput sequencing data, October 27, 2021).
In general, P-value is less robust than effect size. Thus, more researchers prefer to report effect size than to P-value. If sample size is sufficiently large, an effect size of 0.5 or greater is considered more likely corresponding to biological relevance.
A few features have an expected Q-value that is statistically significantly different. They are both relatively rare and have a relatively small difference. For those features, it can be misleading even when identifying them based on the expected effect size. ALDEx2 finds that the safest approach to identify those features is to find where the 95% CI of the effect size does not cross 0. The 95% CI metric behaves exactly in line with intuition: the precision of estimation of rare features is poor. To identify rare features with more confidence, more deep sequencing is required. The authors of ALDEx2 think this 95% CI approach can identify the biological variation in the data as received (i.e., the experimental design is always as given). This is the approach that was used in Macklaim et al. (2013), and it was independently validated to be very robust (Nelson et al. 2015). In summary, this approach is not inferring any additional biological variation but is identifying those features where simple random sampling of the library would be expected to give the same result every time.
2 graphs. An effect size plot of expected P value of Wilcoxon rank sum test versus effect size and a volcano plot of expected P value of Wilcoxon rank sum test versus difference. A dotted line is between 1 e 01 and 1 e 02. Dots for P and B H adjusted values are crowded above the line.
Relationship between effect size, difference, and P-values and BH-adjusted P-values in the tested dataset. This plot shows that the effect size has a much closer relationship to the P-value than does the raw difference
Step 7: Identify significant features by both Welch’s t-test and Wilcoxon rank sum test.
Twenty seven taxa are identified as significant by both Welch’s t-test and Wilcoxon rank sum test, and twelve of these reach significance when the P-values are adjusted for multiple testing corrections using the Benjamini-Hochberg’s method.
The following R commands use the xtable() function from xtable package to make a result table. The xtable package is used to create export tables, converting an R object to an xtable object, which can then be printed as a LaTeX or HTML table. Here, the print.xtable() function is used to export to HTML file. If you want to export the LaTeX file, then use type="latex", file="ALDEx2_Table_Coef_QtRNA.tex" instead.
aldex_all[sig_by_both,c(8:12,1,3,2,4)] is a R object; the element of the object “sig_by_both” is the row of output matrix, the element of the object “c(8:12,1,3,2,4)] is the column of output matrix with the order of columns you want to be in export table.
caption is used to specify the table’s caption or title.
label is used to specify the LaTeX label or HTML anchor.
align indicates the alignment of the corresponding columns and is character vector with the length equal to the number of columns of the resulting table; the resulting table has 9 columns, so the number is 9.
If the R object is a data.frame, the length of align is specified to be 1 + ncol(x) because the row names are printed in the first column.
The left, right, and center alignment of each column are denoted by “l,” “r,” and “c,” respectively. In this table, align=c(“l”,rep(“r”,9) indicates that first column is aligned left, and the remaining 9 columns are aligned right. The digits argument is used to specify the number of digits to display in the corresponding columns (Table 14.1).
The significant features identified by both Welch’s t-test and Wilcoxon rank sum test with P-values and BH-adjusted P-values in the tested dataset
diff.btw | diff.win | effect | effect.low | effect.high | we.ep | wi.ep | we.eBH | wi.eBH | |
|---|---|---|---|---|---|---|---|---|---|
OUT_98 | −4.698 | 3.539 | −1.269 | −9.010 | 0.347 | 0.002 | 0.001 | 0.033 | 0.025 |
OTU_102 | 1.253 | 1.333 | 0.854 | −0.993 | 7.335 | 0.010 | 0.014 | 0.144 | 0.160 |
OTU_116 | −10.435 | 2.831 | −3.563 | −23.145 | −0.797 | 0.000 | 0.000 | 0.000 | 0.001 |
OTU_119 | −3.402 | 1.443 | −2.071 | −16.377 | −0.173 | 0.000 | 0.000 | 0.002 | 0.001 |
OTU_125 | −9.904 | 2.786 | −3.558 | −26.823 | −0.717 | 0.000 | 0.000 | 0.001 | 0.001 |
OTU_126 | −11.171 | 2.684 | −4.260 | −33.527 | −0.944 | 0.000 | 0.000 | 0.000 | 0.001 |
OTU_131 | 3.671 | 1.419 | 2.414 | −0.834 | 18.509 | 0.000 | 0.001 | 0.002 | 0.015 |
OTU_134 | 3.560 | 2.865 | 1.137 | −0.848 | 12.261 | 0.012 | 0.001 | 0.113 | 0.029 |
OTU_135 | 2.528 | 1.235 | 1.938 | 0.198 | 12.070 | 0.000 | 0.000 | 0.003 | 0.002 |
OTU_316 | 4.763 | 3.928 | 1.124 | −1.458 | 10.936 | 0.015 | 0.005 | 0.119 | 0.064 |
OTU_323 | −7.343 | 3.637 | −2.004 | −19.881 | −0.072 | 0.000 | 0.000 | 0.003 | 0.003 |
OTU_342 | 0.639 | 0.830 | 0.725 | −1.801 | 6.394 | 0.041 | 0.043 | 0.332 | 0.322 |
OTU_345 | 0.819 | 0.730 | 1.077 | −0.969 | 7.081 | 0.004 | 0.006 | 0.072 | 0.086 |
OTU_354 | 1.882 | 2.367 | 0.676 | −1.596 | 10.338 | 0.036 | 0.019 | 0.301 | 0.192 |
OTU_359 | 2.107 | 1.420 | 1.244 | −1.761 | 12.310 | 0.002 | 0.005 | 0.043 | 0.081 |
OTU_362 | 2.818 | 1.069 | 2.474 | 0.351 | 14.778 | 0.000 | 0.000 | 0.000 | 0.001 |
OTU_365 | 4.726 | 3.273 | 1.280 | −0.690 | 11.492 | 0.006 | 0.001 | 0.066 | 0.020 |
OTU_371 | 0.889 | 0.909 | 0.820 | −0.746 | 11.161 | 0.013 | 0.005 | 0.177 | 0.080 |
OTU_373 | 2.223 | 2.327 | 0.831 | −1.384 | 10.228 | 0.021 | 0.021 | 0.220 | 0.201 |
OTU_380 | 1.832 | 2.369 | 0.700 | −0.694 | 16.919 | 0.031 | 0.003 | 0.294 | 0.057 |
OTU_385 | 0.513 | 0.397 | 1.265 | −0.371 | 7.901 | 0.001 | 0.001 | 0.019 | 0.025 |
OTU_405 | 0.505 | 0.653 | 0.753 | −1.231 | 7.099 | 0.019 | 0.022 | 0.206 | 0.206 |
OTU_408 | 8.446 | 3.040 | 2.826 | 0.644 | 25.680 | 0.000 | 0.000 | 0.001 | 0.001 |
OTU_410 | −1.393 | 0.776 | −1.742 | −12.694 | −0.161 | 0.000 | 0.000 | 0.002 | 0.002 |
OTU_413 | 0.518 | 0.636 | 0.808 | −1.278 | 6.340 | 0.022 | 0.027 | 0.229 | 0.243 |
OTU_428 | 0.808 | 1.049 | 0.719 | −1.418 | 7.025 | 0.043 | 0.049 | 0.34 | 0.344 |
OTU_448 | −1.122 | 1.311 | −0.887 | −7.396 | 1.385 | 0.010 | 0.011 | 0.144 | 0.142 |
Only those significant taxa detected in both Welch’s t-test and Wilcoxon rank sum tests are printed in Table 14.1. We can interpret the table this way, for the OTU_98, the absolute difference between KO and WT groups can be up to −4.698, implying that the absolute fold change in the ratio between OTU_98 and all other taxa between KO and WT groups for this organism is on average (1/2)−4.698 = 25.96 fold across samples. The difference within the groups of 3.539 is roughly equivalent to the standard deviation, giving an effect size of −4.698/3.539 = −1.327 (here exactly: −1.269 [−9.010, 0.347]).
When running the aldex wrapper, it will link the modular elements together to emulate ALDEx2 prior to the modular approach. In the simplest case, the aldex wrapper performs a two-sample t-test and calculates effect sizes.
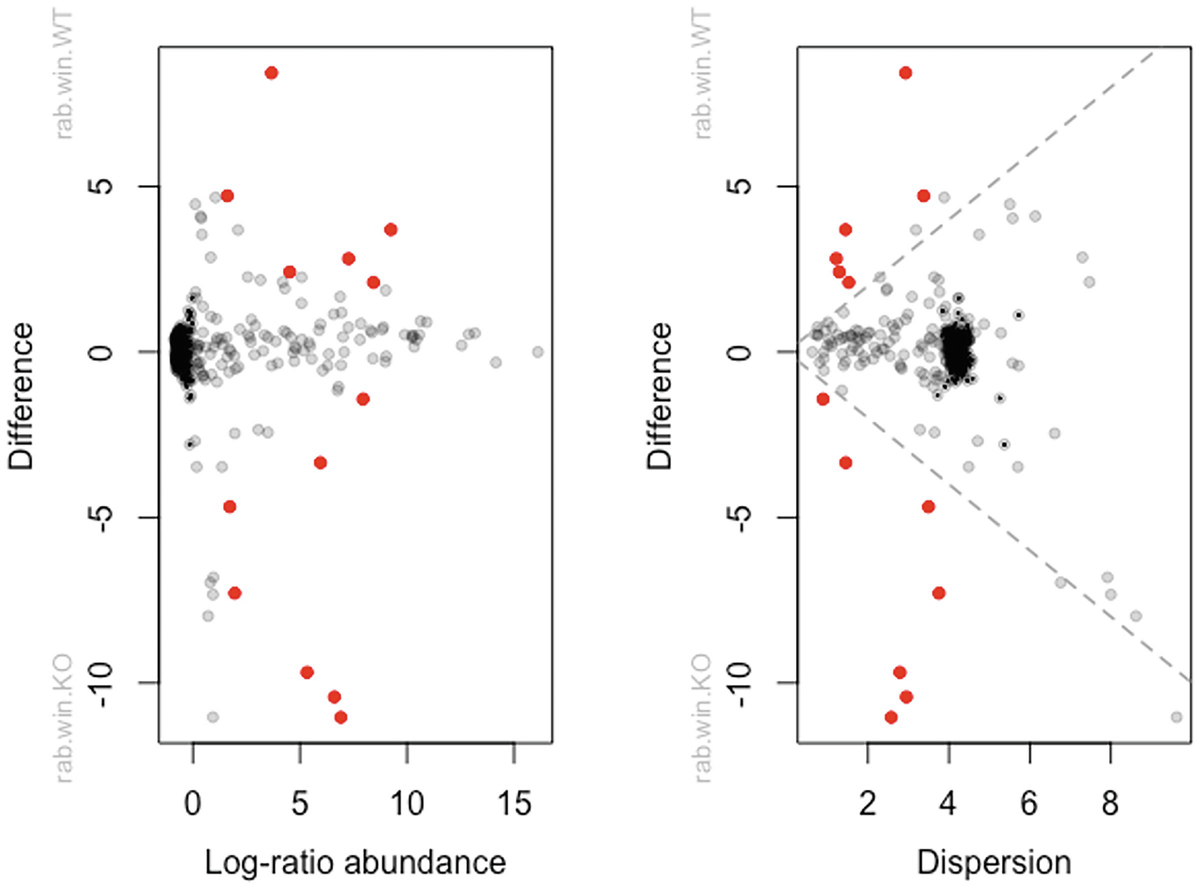
Two scatterplots of difference versus log-ratio abundance and dispersion plots dots in red, gray, and black colors.
MA and MW (effect) plots from t-tests in ALDEx2 output
The inter-quartile log-ratio (iqlr) transformation was introduced in the ALDEx2 package (see Sect. 14.1.6.4). The following commands use iqlr transformation and generate MA and MW plots.
The left panel is an Bland-Altman (MA) plot that shows the relationship between (relative) abundance and difference. The right panel is an MW (effect) plot that shows the relationship between difference and dispersion. In both plots, red dots indicate that the features are statistically significant and gray or black dots indicate the features are not significant. The log-ratio abundance axis is the clr value for the feature.
ALDEx2 also has the aldex.glm module that can be used to implement the probabilistic compositional approach for complex study designs. This module is substantially slower compared to the above two-comparison tests; however, the users can implement their own study designs. Essentially, this approach is same as the above modular approach but requires the users to provide a model matrix and covariates to the glm() function in R.
Here, we use the full dataset from Example 14.1 to illustrate the aldex.glm module. In this dataset, there are two main effect variables Group and Time. We are interested in comparison of the microbiome difference between Group (coded as WT and KO), Time (coded as Before and Post) and their interaction term.
Step 1: Load the count table and metadata.
Step 2: Set model matrix and covariates.
Step 3: Run the aldex.glm() function.
Step 4: Run the aldex.glm.effect () function.
Step 5: Plot the effect sizes.
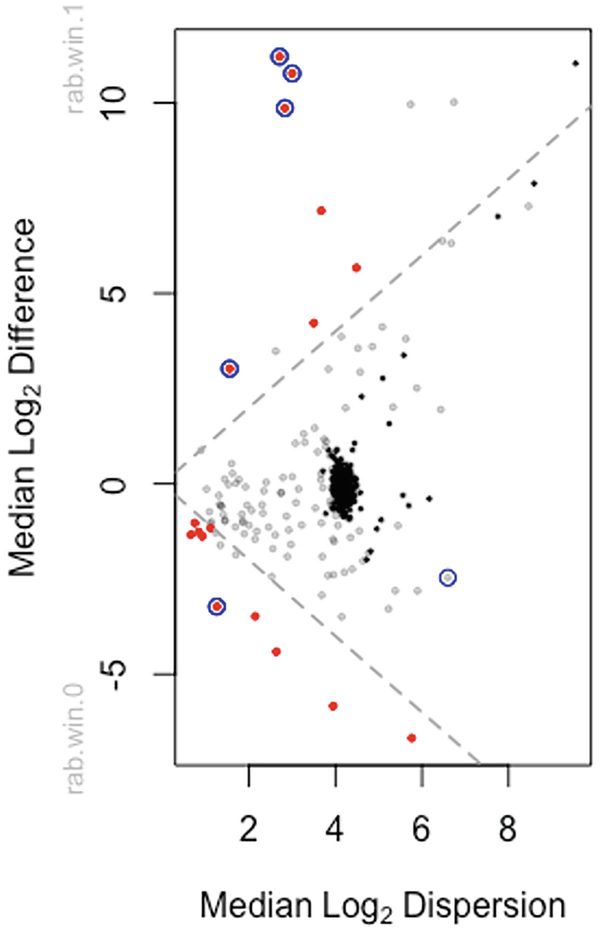
A scatterplot of median log subscript 2 difference versus median log subscript 2 dispersion plots dots in red, gray, and black colors. 2 dotted lines from (0, 0) increase and decrease, respectively.
Plot of effect sizes for Group by Time interaction at post-treatment in breast cancer QTRT1 mouse gut microbiome
Step 6: Write out the glm test and effect table.
First, merge glm and glm effect tests into one object and make a data frame.
The significant features identified by glm test with BH-adjusted P-values in the tested dataset
Group.TimePost.diff.btw | Group.TimePost.diff.win | Group.TimePost.effect | Group.TimePost.overlap | model.Group.TimePost.Pr…t…BH | |
|---|---|---|---|---|---|
OUT_116 | 10.770 | 2.999 | 3.678 | 0.000 | 0.027 |
OTU_119 | 3.022 | 1.552 | 1.787 | 0.031 | 0.012 |
OTU_125 | 9.862 | 2.830 | 3.480 | 0.000 | 0.016 |
OTU_126 | 11.211 | 2.707 | 4.076 | 0.000 | 0.047 |
OTU_362 | −3.225 | 1.255 | −2.480 | 0.002 | 0.013 |
14.2.3 Remarks on ALDEx2
ALDEx2 cannot address zero-inflation problem, instead replaces zero read counts using valid Dirichlet distribution (Fernandes et al. 2013).
ALDEx2 statistical tests are hard to interpret until the log-ratio transformation sufficiently approximate an unchanged reference (Quinn et al. 2018a, b). The performance in this point is dependent on transformations; it was showed that the inter-quartile range log-ratio (iqlr) transformation outperform the centered log-ratio (clr) transformation and was recommended using as the default setting for ALDEx2 (Quinn et al. 2018a, b).
ALDEx2 requires a large number of samples because it performs statistical hypothesis testing using non-parametric methods such as Wilcoxon rank sum test for comparisons of two groups and Kruskal-Wallis test for comparisons of more than two groups. Non-parametric differential expression methods have been suggested reducing statistical power and hence require large number of samples (Quinn et al. 2018a, b; Seyednasrollah et al. 2013; Tarazona et al. 2015; Williams et al. 2017; Quinn et al. 2018a, b). It was reviewed partially due to its non-parametric nature and weaknesses of ALDEx2 methods, the ALDEx2 package has not been widely adopted in the analysis of RNA-seq data (Quinn et al. 2018a, b).
ALDEx2 interprets the log-ratio transformation as a normalization. Thus, ALDEx2 is majorly limited to this normalization. It is hard to interpret the results of the statistical tests even in the setting of large sample sizes when the log-ratio transformation does not sufficiently approximate an unchanged reference (Quinn et al. 2018a, b).
ALDEx2 was reported having difficulty to control FDR (Lin and Peddada 2020b) and to maintain statistical power compared to competing differential abundance methods (e.g., ANCOM, ANCOM-BC, edgeR, and DESeq2) (Lin and Peddada 2020b; Morton et al. 2019).
14.3 Analysis of Composition of Microbiomes (ANCOM)
Like ALDEx2, ANCOM was developed under statistical framework of ANOVA using a non-parametric testing to analyze relative abundance through its log-ratio-transformation of observed counts.
14.3.1 Introduction to ANCOM
ANCOM (Mandal et al. 2015), an alr (additive log-ratio)-based method, was proposed based on alr-transformation to account for the compositional structure of microbiome data. ANCOM repeatedly uses alr-transformation to choose each of the taxa in the dataset as a reference taxon at a time. Thus, given a total of m taxa, ANCOM will choose each of the m taxa to be a reference taxon one time and repeatedly perform the alr-transformation for each taxon and m − 1 regressions. Therefore, total m(m − 1) regression models will be fitted.
Like an ANOVA model, ANCOM models the log-ratios of OTU abundances in each sample with a linear model, but, unlike typical ANOVA, ANCOM accommodates dependencies and correlations among the relative abundances of the OTUs by using of log-ratios. That is, ANCOM lies on framework of ANOVA, while accounts for the compositional structure of microbiome data. The dependencies and hence compositional structure arise in microbiome data because the relative abundances of OTUs sum to 1 or 100% in each sample and because relative abundances of different OTUs may be positively or negatively correlated.
Part 1: Develop a statistical model under the framework of ANOVA to perform compositional differential analysis of each taxon.
Under these two assumptions, for the ith taxon and jth sample, ANCOM developed a statistical model using a standard ANOVA model formulation to perform all possible DA analyses by successively using each taxon as a reference taxon.
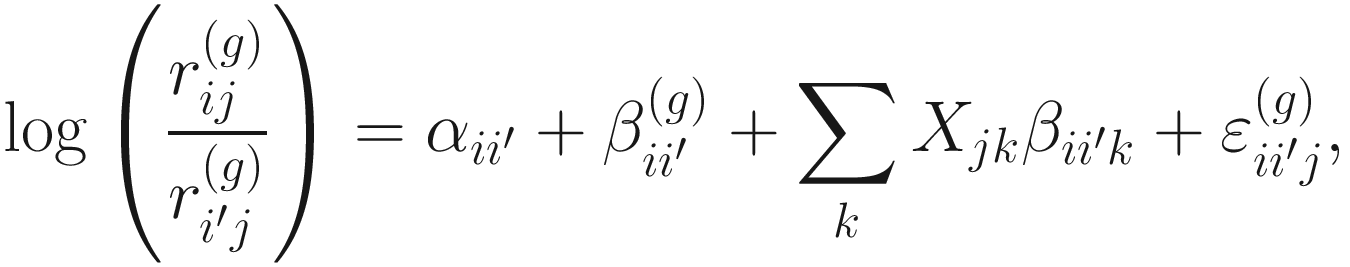
Part 2: Conduct a null hypothesis regarding mean log absolute abundance in a unit volume of an ecosystem using relative abundances.
It was shown (Mandal et al. 2015) that by combining these two assumptions, it can conduct a null hypothesis regarding mean log absolute abundance in a unit volume of an ecosystem using relative abundances. And to test whether a taxon i is differentially abundant regarding a factor of interest with G levels is equivalent to test the null hypothesis and the alternative hypothesis (Lin and Peddada 2020b):
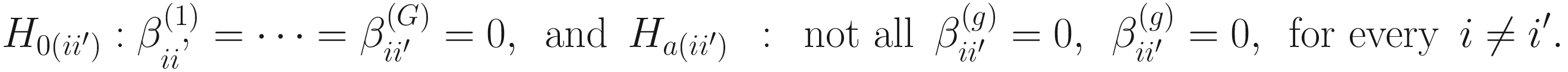
Part 3: Adjust the P-values from the tests of taxon.
There are 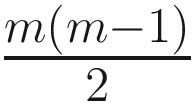 P-values from the
P-values from the 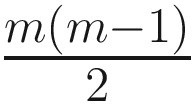 tests of taxon. ANCOM uses Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg 1995) or Bonferroni correction procedure (Dunn 1958, 1961) to adjust the P-values for a multiple testing correction. For each taxon, the number of rejections Wi is based on the empirical distribution of {W1, W2, …, Wm}, which determines the cutoff value of significant taxon (Mandal et al. 2015). The large value of Wi indicates that taxon i is more likely differentially abundant. However, the decision rule of choosing cutoff value of Wi is kind of arbitrary in ANCOM, although 70th percentile of the W distribution is recommended. The users can select different threshold of cutoff value such as the 60th to 90th to output the statistical testing results.
tests of taxon. ANCOM uses Benjamini-Hochberg (BH) procedure (Benjamini and Hochberg 1995) or Bonferroni correction procedure (Dunn 1958, 1961) to adjust the P-values for a multiple testing correction. For each taxon, the number of rejections Wi is based on the empirical distribution of {W1, W2, …, Wm}, which determines the cutoff value of significant taxon (Mandal et al. 2015). The large value of Wi indicates that taxon i is more likely differentially abundant. However, the decision rule of choosing cutoff value of Wi is kind of arbitrary in ANCOM, although 70th percentile of the W distribution is recommended. The users can select different threshold of cutoff value such as the 60th to 90th to output the statistical testing results.
14.3.2 Implement ANCOM Using QIIME 2
These mouse gut microbiome datasets were generated by DADA2 within QIIME 2 from raw 16S rRNA sequencing data and have been used for illustrating statistical analyses of alpha and beta diversities, as well other analyses and plots via QIIME 2 in Chaps. 9, 10, and 11. Here, we continue to use these datasets to illustrate implementation of ALDEx2 using QIIME 2. We showed in Chap. 10 via emperor plot that a lot of features were changed in abundance over time (Early and Late times). In this section, we illustrate how to test differential abundances with ANCOM using the same mouse gut data in Example 9.2.
Step 1: Use the filter-samples command to filter feature table.
ANCOM assumes that less than about 25% of the features are changing between groups. If this assumption is violated, then ANCOM will be more possible to increase both Type I and Type II errors. As we showed in Chap. 10 via emperor plot that a lot of features were changed in abundance over time (Early and Late times), here we will filter the full feature table to only contain late mouse gut samples and then perform ANCOM to identify which sequence variants and taxa are differentially abundant across the male and female mouse gut samples.

A text reads, saved feature table, open bracket, frequency, close bracket, to, L a t e M o u s e G u t T a b l e dot q z a.

A text reads, saved feature table, open bracket, frequency, close bracket, to, L a t e M o u s e G u t T a b l e 2 dot q z a.

A text reads, saved feature table, open bracket, frequency, close bracket, to, L a t e M o u s e G u t T a b l e 3 dot q z a.
Step 2: Use taxa collapse command to collapse feature table

A text reads, saved feature table, open bracket, frequency, close bracket, to, L a t e M o u s e G u t T a b l e L 6 dot q z a.
A text reads, saved feature table, open bracket, frequency, close bracket, to, L a t e M o u s e G u t T a b l e L 7 dot q z a.
The following intermediate files can be removed from the directory by rm command, such as rm LateMouseGutTable.qza. However, we keep them there for later review.
Step 3: Use the add-pseudocount command to add a small pseudocount to produce the compositional feature table artifact.
As a compositional method, ANCOM cannot address zero issue because frequencies of zero are not defined when taking log or log-ratio transformation. ANCOM operates on a FeatureTable[Composition] QIIME 2 artifact, which is based on frequencies of features on a per-sample basis. To build the composition artifact (a FeatureTable[Composition] artifact), a small pseudocount must be added to the FeatureTable[Frequency] artifact typically via an imputation method.

A text reads, saved feature table, open bracket, composition, close bracket, to, C o m p L a t e M o u s e G u t T a b l e L 6 dot q z a.

A text reads, saved feature table, open bracket, composition, close parenthesis, to, C o m p L a t e M o u s e G u t T a b l e L 7 dot q z a.
Step 4: Perform ANCOM to identity differential features across the mouse gut sex groups.

A text reads, saved visualization to, A n c o m S e x M i s S e q underscore S O P L 6 dot q z v.

A text reads, saved visualization to, A n c o m S e x M i s S e q underscore S O P L 7 dot q z v.
qiime tools view
 A text reads, A n c o m S e x M i s S e q underscore S O P L 7 dot q z v.
A text reads, A n c o m S e x M i s S e q underscore S O P L 7 dot q z v.
This view command displays three results: (1) ANCOM Volcano Plot, (2) ANCOM statistical results, and (3) percentile abundances of features by group. All these results can be exported, downloaded, and saved.
Abundant and not abundant taxa identified by ANCOM statistical testing
Kingdom | Phylum | Class | Order | Family | Genus | Species | W | Reject null hypothesis |
|---|---|---|---|---|---|---|---|---|
k__Bacteria | p__Firmicutes | c__Bacilli | o__Lactobacillales | f__Lactobacillaceae | g__Lactobacillus | s__ | 48 | TRUE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Clostridiaceae | __ | __ | 48 | TRUE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Peptococcaceae | g__rc4-4 | s__ | 47 | TRUE |
k__Bacteria | p__Actinobacteria | c__Actinobacteria | o__Bifidobacteriales | f__Bifidobacteriaceae | g__Bifidobacterium | s__pseudolongum | 44 | TRUE |
k__Bacteria | p__Verrucomicrobia | c__Verrucomicrobiae | o__Verrucomicrobiales | f__Verrucomicrobiaceae | g__Akkermansia | s__muciniphila | 44 | TRUE |
k__Bacteria | p__TM7 | c__TM7-3 | o__CW040 | f__F16 | g__ | s__ | 38 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Lactobacillales | f__Lactobacillaceae | g__Lactobacillus | __ | 35 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Turicibacterales | f__Turicibacteraceae | g__Turicibacter | s__ | 35 | FALSE |
k__Bacteria | p__Proteobacteria | c__Gammaproteobacteria | o__Pseudomonadales | f__Pseudomonadaceae | g__Pseudomonas | s__veronii | 25 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | __ | __ | __ | 23 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__[Mogibacteriaceae] | g__ | s__ | 18 | FALSE |
k__Bacteria | p__Tenericutes | c__Mollicutes | o__RF39 | f__ | g__ | s__ | 17 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__Dorea | s__ | 16 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | g__Oscillospira | s__ | 14 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__ | s__ | 14 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__ | g__ | s__ | 14 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | g__Butyricicoccus | s__pullicaecorum | 13 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Dehalobacteriaceae | g__Dehalobacterium | s__ | 13 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__Clostridium | s__colinum | 12 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | g__Clostridium | s__methylpentosum | 12 | FALSE |
k__Bacteria | p__Firmicutes | c__Erysipelotrichi | o__Erysipelotrichales | f__Erysipelotrichaceae | g__Allobaculum | s__ | 12 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | g__ | s__ | 11 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | __ | __ | 11 | FALSE |
k__Bacteria | p__Tenericutes | c__Mollicutes | o__Anaeroplasmatales | f__Anaeroplasmataceae | g__Anaeroplasma | s__ | 10 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | __ | __ | 10 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__Roseburia | s__ | 10 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Christensenellaceae | g__ | s__ | 10 | FALSE |
k__Bacteria | p__[Thermi] | c__Deinococci | o__Deinococcales | f__Deinococcaceae | g__Deinococcus | s__ | 9 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Clostridiaceae | g__Clostridium | s__butyricum | 9 | FALSE |
k__Bacteria | p__Firmicutes | c__Erysipelotrichi | o__Erysipelotrichales | f__Erysipelotrichaceae | g__Coprobacillus | s__ | 9 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Bacillales | f__Staphylococcaceae | g__Staphylococcus | __ | 9 | FALSE |
k__Bacteria | p__Proteobacteria | c__Betaproteobacteria | o__Neisseriales | f__Neisseriaceae | g__Neisseria | s__cinerea | 9 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__Blautia | __ | 9 | FALSE |
k__Bacteria | p__Proteobacteria | c__Gammaproteobacteria | o__Pseudomonadales | f__Moraxellaceae | g__Acinetobacter | s__guillouiae | 9 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Bacillales | f__Staphylococcaceae | g__Jeotgalicoccus | s__psychrophilus | 9 | FALSE |
k__Bacteria | p__Proteobacteria | c__Alphaproteobacteria | o__Rickettsiales | f__mitochondria | __ | __ | 9 | FALSE |
k__Bacteria | p__Proteobacteria | c__Gammaproteobacteria | o__Enterobacteriales | f__Enterobacteriaceae | __ | __ | 9 | FALSE |
k__Bacteria | p__Bacteroidetes | c__Bacteroidia | o__Bacteroidales | f__Bacteroidaceae | g__Bacteroides | s__ovatus | 9 | FALSE |
k__Bacteria | p__Actinobacteria | c__Coriobacteriia | o__Coriobacteriales | f__Coriobacteriaceae | __ | __ | 8 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Lactobacillales | f__Streptococcaceae | g__Streptococcus | s__ | 8 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Clostridiaceae | g__Candidatus Arthromitus | s__ | 8 | FALSE |
k__Bacteria | p__Firmicutes | c__Bacilli | o__Lactobacillales | f__Lactobacillaceae | g__Lactobacillus | s__reuteri | 7 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__[Ruminococcus] | s__gnavus | 7 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Ruminococcaceae | g__Ruminococcus | s__ | 7 | FALSE |
k__Bacteria | p__Firmicutes | c__Clostridia | o__Clostridiales | f__Lachnospiraceae | g__Coprococcus | s__ | 7 | FALSE |
k__Bacteria | p__Actinobacteria | c__Coriobacteriia | o__Coriobacteriales | f__Coriobacteriaceae | g__ | s__ | 6 | FALSE |
k__Bacteria | p__Cyanobacteria | c__Chloroplast | o__Streptophyta | f__ | g__ | s__ | 6 | FALSE |
k__Bacteria | p__Actinobacteria | c__Coriobacteriia | o__Coriobacteriales | f__Coriobacteriaceae | g__Adlercreutzia | s__ | 5 | FALSE |
k__Bacteria | p__Bacteroidetes | c__Bacteroidia | o__Bacteroidales | f__Rikenellaceae | g__ | s__ | 5 | FALSE |
k__Bacteria | p__Bacteroidetes | c__Bacteroidia | o__Bacteroidales | f__S24-7 | g__ | s__ | 5 | FALSE |

A text reads, saved feature table open bracket, composition, close bracket, to, c o m p L a t e M o u s e G u t T a b l e dot q z a.

A text reads, saved visualization to, A n c o m S e x M i s S e q underscore S O P dot q z v.
ANCOM provides two optional parameters --p-transform-function and --p-difference-function to perform identity differential features. Both parameters are TEXT choices [(‘sqrt’, ‘log’, ‘clr’), (‘mean_difference’, ‘f_statistic’) for --p-transform-function and --p-difference-function, respectively]. The transform-function is used to specify the method to transform feature values before generating volcano plots. The default is “clr” (centered log ratio-transformation). Other two are square root (“sqrt”) and log (“log”) transformations. The difference-function is used to specify the method to visualize fold difference in feature abundances across groups for volcano plots. One command is provided below.

A text reads, saved visualization to, A n c o m S e x M i s S e q underscore S O P L 7 dot q z v.
14.3.3 Remarks on ANCOM
- It was shown that ANCOM has well controlled the FDR while maintaining power comparable with other methods (Mandal et al. 2015; Lin and Peddada 2020a). However, like ALDEx2, ANCOM actually uses log-ratio transformations as a kind of normalization (log-ratio “normalizations”). Thus, ANCOM suffers from some similar limitations as ALDEx2:
Its usefulness mainly depends on interpreting the log-ratio transformation as a normalization. In other words, the statistical tests can be appropriately interpreted only when the log-ratio transformation sufficiently approximates an unchanged reference (Quinn et al. 2018a, b). In contrast, it was reviewed that the methods that do not require using log-ratio transformations as a kind of normalization are more appropriate (Quinn et al. 2018a, b).
Cannot address zero-inflation problem, instead adds an arbitrary small pseudocount value such as 0.001, 0.5, or 1 to all read counts. This indicates compositional analysis approach fails in the presence of zero values (Xia et al. 2018a, p. 389). It was shown that due to improper handling of the zero counts, ANCOM inflated the number of false positives instead of controlled the false-positive rate (FDR) (Brill et al. 2019).
It is underpowered and requires a large number of samples due to using non-parametric testing (Quinn et al. 2018a, b) as well as has decreased sensitivity on small datasets (e.g., less than 20 samples per group) partially because of its non-parametric nature (i.e., Mann-Whitney test) (Weiss et al. 2017; Quinn et al. 2018a, b).
- Specifically, ANCOM has other weaknesses, including:
ANCOM takes the approach of alr-transformation and transforms the observed abundances of each taxon to log-ratios of the observed abundance relative to a pre-specified reference taxon. Because when performing differential abundance analysis, typically, the comparing samples have thousands of taxa in microbiome data sets. Thus, it is computationally intensive to repeatedly apply alr-transformation to each taxon in the dataset as a reference taxon. The choice of this reference taxon is also a challenge when the number of taxa is large.
Whether ANCOM can control FDR well or not, different studies have reported inconsistent results: some different simulation studies reported that ANCOM can control FDR reasonably well under various scenarios (Lin and Peddada 2020a; Weiss et al. 2017), whereas other studies reported that ANCOM could generate a potential false-positive result when a cutoff of 0.6 was used for the W statistic (Morton et al. 2019). Thus, when ANCOM is used in differential abundance analysis, a stricter cutoff value for the W statistic is recommended to reduce the chance of false positives.
ANCOM uses the quantile of its test statistic W instead of P-values to conduct statistical testing for significance. This not only makes the analysis results difficult to interpret (Lin and Peddada 2020b) but also does not make ANCOM to improve its performance by filtering taxa before analysis. ANCOM was reported having reduced the number of detected differential abundant taxa. This is most likely related to the way that W statistics are calculated and used for significance in ANCOM (Wallen 2021).
ANCOM does not provide P-value for individual taxon and cannot provide standard errors or confidence intervals of DA for each taxon (Lin and Peddada 2020a).
It is difficult to interpret the testing differential abundance results because ANCOM uses presumed invariant features to guide the log-ratio transformation (Quinn et al. 2018a, b).
14.4 Analysis of Composition of Microbiomes-Bias Correction (ANCOM-BC)
ANCOM-BC is a bias correction version of ANCOM (analysis of compositions of microbiomes).
14.4.1 Introduction to ANCOM-BC
ANCOM-BC (Lin and Peddada 2020a) was proposed for differential abundance (DA) analysis of microbiome data with bias correction to ANCOM. ANCOM-BC was developed under the assumptions that (1) the observed abundance in a feature table is expected to be proportional to the unobservable absolute abundance of a taxon in a unit volume of the ecosystem. (2) The sampling fraction varies from sample to sample and hence inducing the estimation bias. Thus, to address the problem of unequal sampling fractions, ANCOM-BC uses a sample-specific offset term to serve as the bias correction (Lin and Peddada 2020a). The offset term is usually used in the generalized linear models such as Poisson, zero-inflated models to adjust for the sampling population (Xia et al. 2018b). Here ANCOM-BC uses a sample-specific offset term in a linear regression framework.
Part 1: Define the sample-specific sampling fraction.
Unlike some other DA studies, which defines relative abundances of taxa as frequencies of these taxa in a sample, in ANCOM-BC, relative abundance of a taxon in the sample refers to the fraction of the taxon observed in the feature table relative to the sum of all observed taxa corresponding to the sample in the feature table (Lin and Peddada 2020a, b). Actually, it is the proportion of this taxon relative to the sum of all taxa in the sample with range of (0, 1). In ANCOM-BC, absolute abundance is defined as unobservable actual abundance of a taxon in a unit volume of an ecosystem, while observed abundance refers to the observed counts of features (OTUs or ASVs) in the feature table (Lin and Peddada 2020b).
Let Oij denote the observed abundance of ith taxon in jth sample, Aij the unobserved abundance of ith taxon in the ecosystem of ith sample, and then the sample-specific sampling fraction cj is defined as:
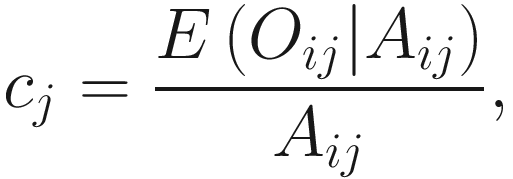
Part 2: Describe two model assumptions of ANCOM-BC.
Assumption 1 is given below.
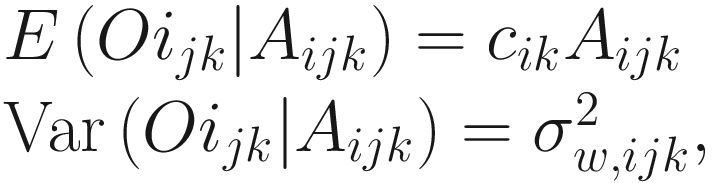
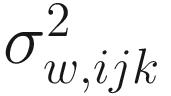 is the variability between specimens within the kth sample from the jth group, which characterizes the within-sample variability. Usually the within-sample variability is not estimated since typically at a given time only one specimen is available in most microbiome studies. The assumption in (14.12) states that the absolute abundance of a taxon in a random sample is expected to be in constant proportion to the absolute abundance in the ecosystem of the sample. That is, the expected relative abundance of each taxon in a random sample equals to the relative abundance of the taxon in the ecosystem of the sample (Lin and Peddada 2020a).
is the variability between specimens within the kth sample from the jth group, which characterizes the within-sample variability. Usually the within-sample variability is not estimated since typically at a given time only one specimen is available in most microbiome studies. The assumption in (14.12) states that the absolute abundance of a taxon in a random sample is expected to be in constant proportion to the absolute abundance in the ecosystem of the sample. That is, the expected relative abundance of each taxon in a random sample equals to the relative abundance of the taxon in the ecosystem of the sample (Lin and Peddada 2020a).
 is the between-sample variation within group j for the ith taxon. The assumption in (14.13) states that for a given taxon, all subjects within and between groups are independent.
is the between-sample variation within group j for the ith taxon. The assumption in (14.13) states that for a given taxon, all subjects within and between groups are independent.Combining Assumption 1 in (14.12) and Assumption 2 in (14.13), the expected and variance of Oijk are defined as:
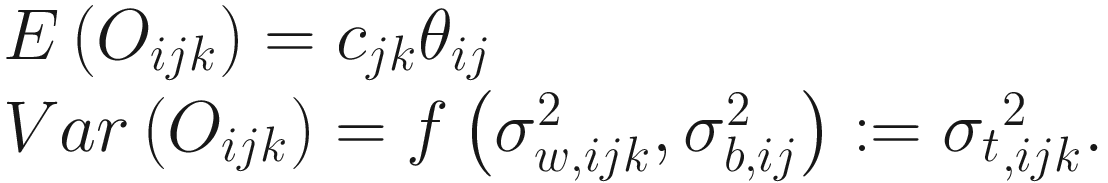
Part 3: Introduce a linear regression model framework for log-transformed OTU counts data to include the sample specific bias due to sampling fractions.
Under the above setting, the linear model framework for log-transformed OTU counts data is written as below.

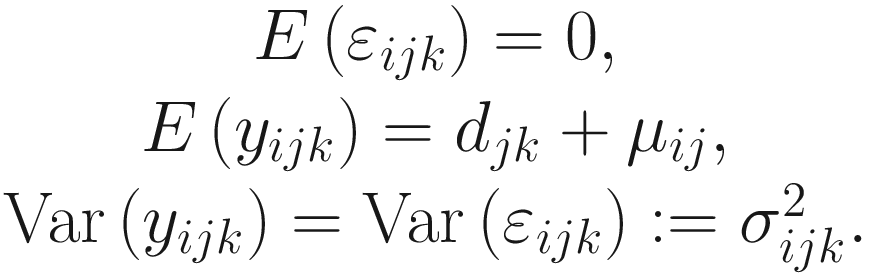
Part 4: Develop a linear regression model that estimate the sample-specific bias and ensure that the estimator and the test statistic are asymptotically centered at zero under the null hypothesis.
Since the sample-specific bias is introduced because of the differential sampling fraction by each sample, thus, the goal of ANCOM-BC is to eliminate this bias. Given a large number of taxa on each subject, to estimate this bias, ANCOM-BC borrows information across taxa in its methodology.
The framework of least squares was used to develop bias and variance of bias estimation under the null hypothesis, which are estimated as follows.
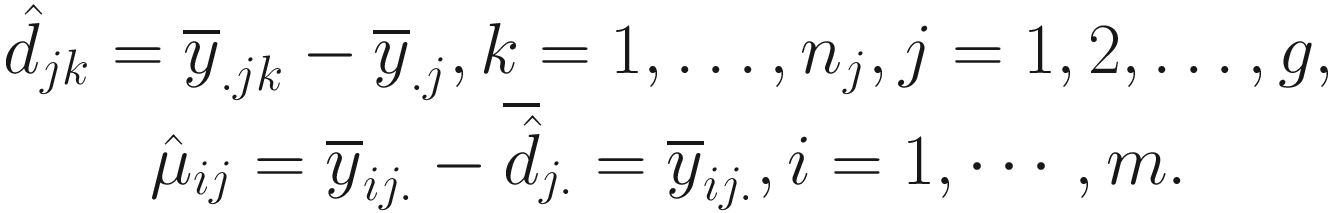
 . Thus, for each j = 1, 2, …, g, Lin and Peddada (2020a) approve that
. Thus, for each j = 1, 2, …, g, Lin and Peddada (2020a) approve that 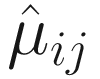 is a biased estimator and
is a biased estimator and 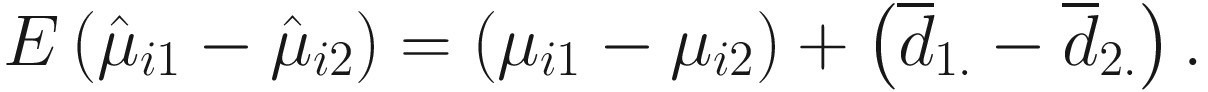 For two experimental groups with balanced design (i.e., g = 2 and n1 = n2 = n) and given two ecosystems, for each taxon i, i = 1, ⋯, m, the test hypotheses are
For two experimental groups with balanced design (i.e., g = 2 and n1 = n2 = n) and given two ecosystems, for each taxon i, i = 1, ⋯, m, the test hypotheses are 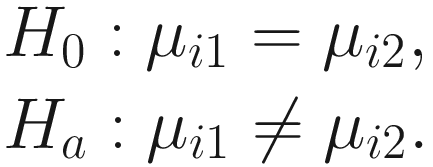
By denoting 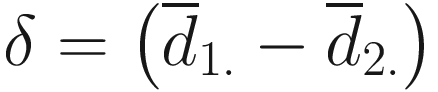 , under the null hypothesis,
, under the null hypothesis, 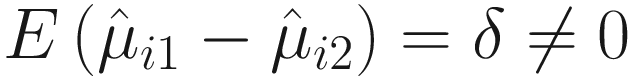 and hence is biased. From (12.15) and Lyapunov central limit theorem, Lin and Peddada (2020a) show that
and hence is biased. From (12.15) and Lyapunov central limit theorem, Lin and Peddada (2020a) show that
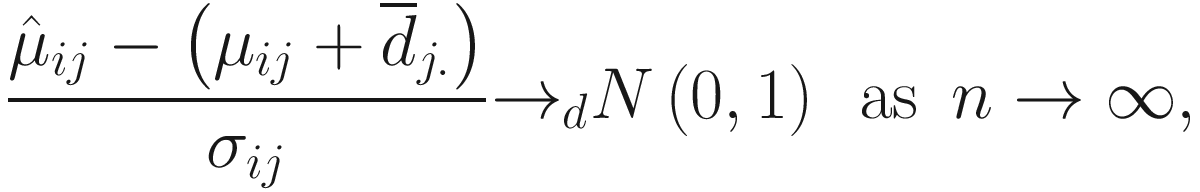
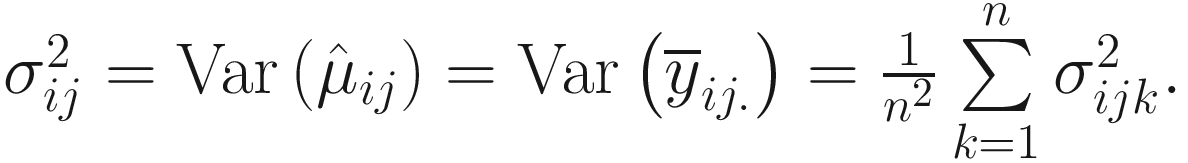 Lin and Peddada (2020a) show that the taxa can be modeled using a Gaussian mixtures model and the expectation-maximization (EM) algorithm (i.e.,
Lin and Peddada (2020a) show that the taxa can be modeled using a Gaussian mixtures model and the expectation-maximization (EM) algorithm (i.e.,  , which denotes the resulting estimator of δ). They also show that that
, which denotes the resulting estimator of δ). They also show that that  and
and 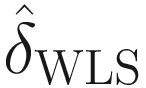 (denoting the weighted least squares (WLS) estimator of δ) are highly correlated, are approximately unbiased, and thus can use
(denoting the weighted least squares (WLS) estimator of δ) are highly correlated, are approximately unbiased, and thus can use 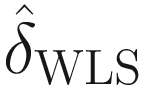 to approximate for
to approximate for  .
.Therefore, under some further assumptions and developments, for hypothesis testing for two-group comparison: 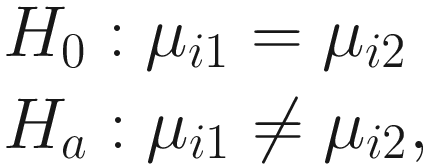 for taxon i , the following test statistic is approximately centered at zero under the null hypothesis:
for taxon i , the following test statistic is approximately centered at zero under the null hypothesis:
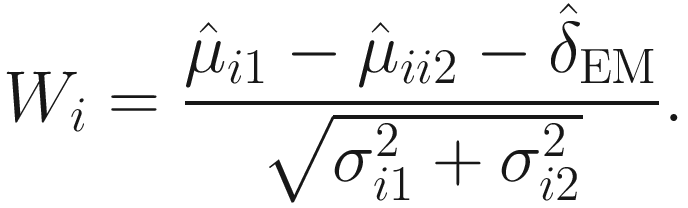
From Slutsky’s theorem,
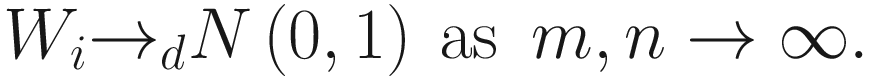
The above test statistic is modified as follows if the sample size is not very large and/or the number of non-null taxa is very large:
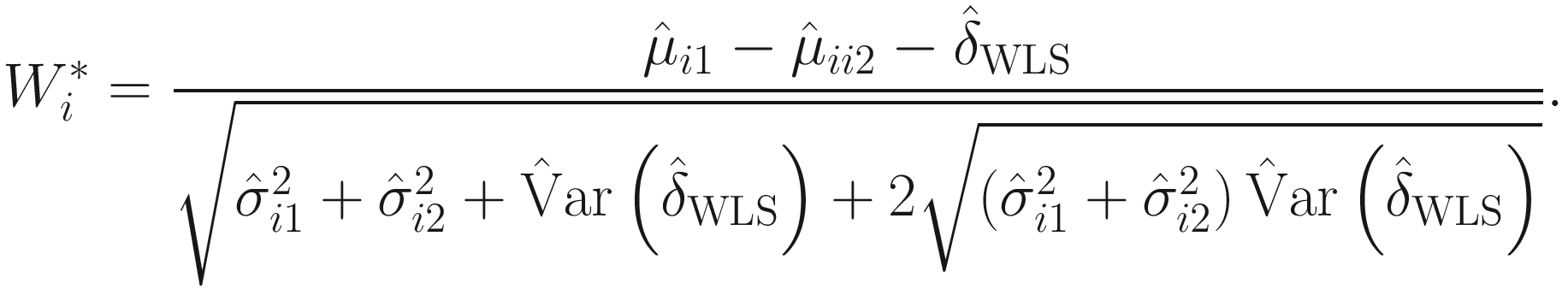
Part 5: Adjust the P-values from the tests of taxon.
Part 6: Develop the test statistic for hypothesis testing for multigroup comparison to conduct the global test.
The test statistic for multigroup comparison was developed in the same way to the two-group comparison. That is, first getting the initial estimates of 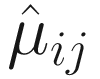 and
and 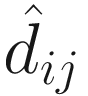 , then setting the reference group r (e.g., r = 1), and obtaining the estimator of the bias term
, then setting the reference group r (e.g., r = 1), and obtaining the estimator of the bias term 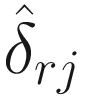 through E-M algorithm, the final estimator of mean absolute abundance of the ecosystem (in log scale) are obtained by transforming
through E-M algorithm, the final estimator of mean absolute abundance of the ecosystem (in log scale) are obtained by transforming 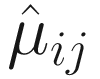 of (14.17) into:
of (14.17) into:
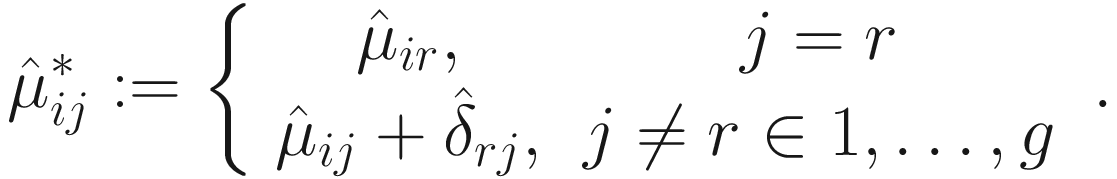
The test statistic for pairwise comparison is defined as:
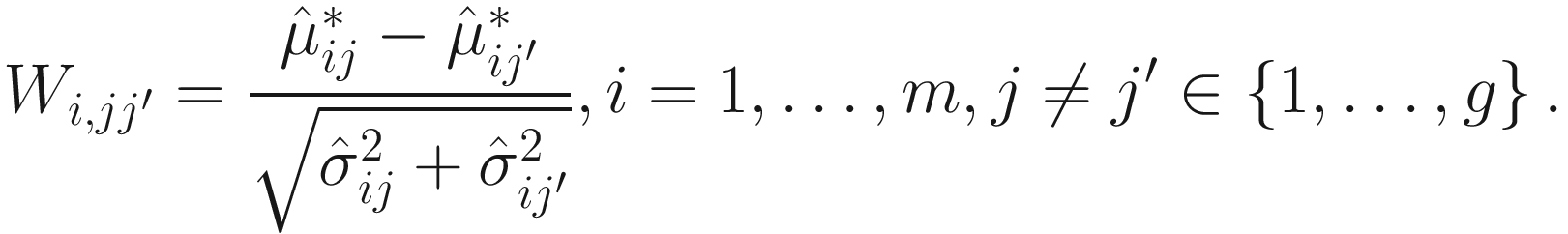
For computational simplicity, the global test statistic is reformulated based on William’s type of test (Williams 1971, 1977; Peddada et al. 2001; Farnan et al. 2014) as follows:
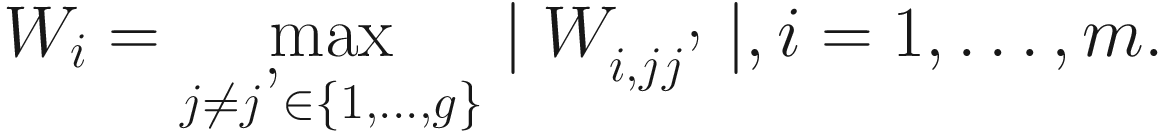
Under null, Wi, jj'→dN(0, 1), thus for each specific taxon i, the null distribution of Wi can be constructed by simulations. Finally, P-value is calculated as:
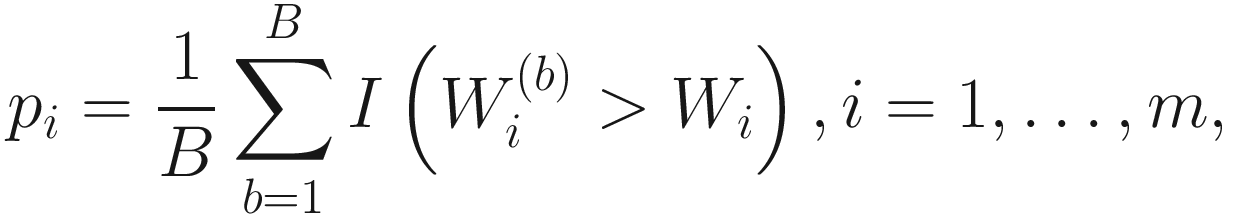
14.4.2 Implement ANCOM-BC Using the ANCOMBC Package
ANCOM-BC method is implemented via the ancombc () function in the ANCOMBC package. This package was developed to identify those taxa that their absolute abundances per unit volume in the ecosystem (e.g., gut, mouth or vagina) are differentially abundant between treatment groups/conditions while allowing adjustment of other covariates of interest. In current version (ANCOM-BC (v.1.2.2), October 2021), ANCOM-BC is performed for cross-sectional data.
One syntax is given as:
phyloseq is a phyloseq-class object, consisting of a feature (OUT/ASV) table (in ANCOM-BC, refers to microbial observed abundance table), a sample metadata, a taxonomy table (optional), and a phylogenetic tree (optional). As we described in Chap. 2, to create a phyloseq-class object, the row names of the metadata must match the sample names of the feature table, and the row names of the taxonomy table must match the taxon (feature) names of the feature table.
formula is a the character string expression. It is used to specify how the microbial absolute abundances for each taxon (response variable) depend on the variables in metadata (predictor variables or covariates) such as we can specify that formula = “Age + Gender + BMI + Group”.
p_adj_method is used to specify the method for adjusting P-values. The default method is “holm” (Holm 1979). The optional methods include “holm”, “hochberg” (Hochberg 1988), “hommel” (Hochberg 1988), “bonferroni” (Bonferroni 1936), “BH” or its alias “fdr” (Benjamini and Hochberg 1995), “BY” (Benjamini and Yekutieli 2001), and “none.” Tukey’s method is not available in this package. Type ?p.adjust() to check the options and references in R. If you do not want to adjust the P-value, use the pass-through option (“none”).
zero_cut is a numerical fraction with range of (0, 1). It is used to specify the proportion of zero values for taxa greater than the cutoff values will be excluded in the analysis. Default is 0.90.
lib_cut is used to specify a numerical threshold for filtering samples based on library sizes. Samples with library sizes less than this cutoff values will be excluded in the analysis. Default is 0, without filtering any sample.
group is the group variable in metadata. It is required for detecting structural zeros and performing global test.
struc_zero is used to specify whether to detect structural zeros. Default is FALSE.
neg_lb is used to specify to classify a taxon as a structural zero in the corresponding study group using its asymptotic lower bound. Default is FALSE.
tol is the iteration convergence tolerance for the E-M algorithm. Default is 1e-05.
max_iter is used to specify the maximum number of iterations for the E-M algorithm. Default is 100.
conserve is used to specify a conservative variance estimate of the test statistic. Default is FALSE. Because ANCOM-BC may not perform well when the sample sizes are very small (e.g., n ≤ 5 per group) or when the proportion of differentially abundant taxa is too large (e.g., >75%) (Lin and Peddada 2020a), it is recommended to use in the case of small sample size and/or large number of differentially abundant taxa.
alpha is used to specify the level of significance. Default is 0.05.
global is used to specify a global test. Default is FALSE.
First, type the following commands to download, install, and load the ANCOMBC package.
Then, load OTU-table, taxonomy table, and sample metadata.
Next, create a phyloseq-class object.
Finally, implement the ancombc() function to perform primary analysis and global test.
We can specify global = TRUE to request both global test and primary analysis.
ANCOMBC Primary Analysis.
The following commands request only the primary analysis.
- 1)
res$beta (coefficients: a data.frame of coefficients).
- 2)
res$se (standard errors: a data.frame of standard errors (SEs) of beta).
- 3)
res$W(test statistics: a data.frame of test statistics. W = beta/se).
- 4)
res$p_val (P-values: a data.frame of P-values obtained from two-sided Z-test using the test statistic W).
- 5)
res$q_val (adjusted P-values: a data.frame of adjusted P-values obtained by applying the p_adj_method to p_val).
- 6)
res$diff_abn (differentially abundant taxon indicators: a logical data.frame. TRUE if the taxon has q_val less than alpha otherwise FALSE).
res$feature_table: a data.frame of pre-processed (based on zero_cut and lib_cut) microbial observed abundance table).
res$zero_ind: a logical matrix with TRUE indicating the taxon is identified as a structural zero for the specified group variable.
res$samp_frac: a numeric vector of estimated sampling fractions in log scale (natural log)).
res$resid: a matrix of residuals from the ANCOM-BC log-linear (natural log) model. Rows are taxa and columns are samples.
res$delta_em: estimated bias terms through E-M algorithm.
res$delta_wls: estimated bias terms through weighted least squares (WLS) algorithm.
Microbiome data may exist three kinds of zeros: structural zeros, sampling zeros, and rounded zeros. Their definitions can be found in Xia et al. (2018c) and the strategies of dealing with them in compositional microbiome data have been described in Xia et al. (2018a).
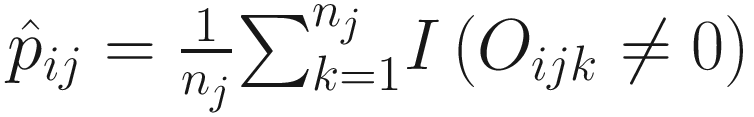 denote the estimate of pij. Then the ith taxon is declared to exist structural zeros in the jth group if either of the following is true.
denote the estimate of pij. Then the ith taxon is declared to exist structural zeros in the jth group if either of the following is true.- 1.
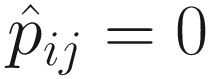 .
. - 2.
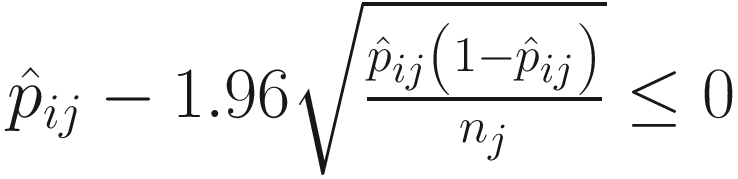 .
.
If a taxon is declared to be a structural zero in an experimental group, then, for that specific ecosystem, ANCOM-BC does not include this taxon in the analysis (Lin and Peddada 2020a). To apply both criteria stated in above definitions of structural zeros, set neg_lb = TRUE; otherwise, ANCOM-BC uses only Equation 1 to declare structural zeros. Setting neg_lb = TRUE is recommended when the sample size per group is relatively large (e.g., >30).
We create the object “rest_primary” to present the primary results(output$res) for operation.
> rest_primary = output$res
Step 1: Obtain the estimated coefficients of beta.
The estimated coefficients of beta in QtRNA microbiome data
Kingdom | Phylum | Class | Order | Family | Genus | Species | Group | TimePost | Group:TimePost | |
|---|---|---|---|---|---|---|---|---|---|---|
OTU_56 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus caecimuris B7 | 0.000463 | 0.049312 | 0.012773 |
OTU_57 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus muris | 0.856548 | 0.604616 | −0.83636 |
OTU_58 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__mouse gut metagenome | −0.35507 | 1.136966 | −0.0586 |
OTU_77 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Bacteroidaceae | D_5__Bacteroides | D_6__Bacteroides acidifaciens JCM 10556 | −0.06885 | 0.389432 | −0.32735 |
OTU_101 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Muribaculaceae | D_5__Muribaculum | D_6__Parabacteroides sp. YL27 | 0.000463 | 0.118627 | 3.06081 |
OTU_131 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Tannerellaceae | D_5__Parabacteroides | D_6__Parabacteroides goldsteinii CL02T12C30 | −0.8368 | −1.42599 | −1.49273 |
OTU_221 | D_0__Bacteria | D_1__Cyanobacteria | D_2__Oxyphotobacteria | D_3__Nostocales | D_4__Nostocaceae | Other | Other | 0.375805 | 0.326571 | −0.5012 |
OTU_263 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus saprophyticus subsp. saprophyticus | −0.13817 | −0.47644 | 0.220717 |
OTU_264 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus sp. UAsDu23 | −0.93095 | −1.7192 | 1.013497 |
OTU_276 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__Lactobacillus murinus | 0.139093 | 0.257256 | −0.3338 |
OTU_279 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__gut metagenome | 0.103425 | 0.106848 | −0.3338 |
OTU_287 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Streptococcaceae | D_5__Streptococcus | D_6__Streptococcus danieliae | −0.25306 | 0.840292 | 0.151861 |
OTU_323 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__ASF356 | D_6__Clostridium sp. ASF356 | 0.000463 | −0.02 | 3.469499 |
OTU_325 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Acetatifactor | D_6__Clostridiales bacterium CIEAF 015 | 0.156511 | −2.28364 | −0.26737 |
OTU_330 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Anaerostipes | D_6__Clostridiales bacterium VE202−09 | −0.11611 | −0.50183 | −0.3425 |
OTU_351 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Clostridiales bacterium CIEAF 020 | 0.748644 | 0.79693 | −1.77908 |
OTU_353 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium A4 | −0.0377 | −0.42619 | −0.44784 |
OTU_354 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium COE1 | 1.068315 | 0.69781 | −2.21009 |
OTU_361 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae UCG-006 | D_6__Clostridium sp. ASF502 | −0.30308 | −0.63509 | −0.45926 |
OTU_366 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Marvinbryantia | D_6__Clostridiales bacterium CIEAF 012 | −0.03092 | 0.015579 | −0.63559 |
OTU_369 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Clostridium sp. Clone-44 | 0.248954 | −0.02 | −0.30503 |
OTU_370 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Eubacterium sp. 14-2 | −1.37716 | −2.75447 | 1.538724 |
OTU_395 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Anaerotruncus | D_6__Anaerotruncus sp. G3(2012) | 0.133685 | −1.46779 | 0.071386 |
OTU_408 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Clostridium sp. Culture Jar-8 | 0.000463 | 4.359209 | −4.29712 |
OTU_409 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Ruminiclostridium sp. KB18 | 0.564388 | 2.346951 | −1.2909 |
OTU_412 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 9 | D_6__bacterium enrichment culture clone M244 | −0.34294 | 1.211262 | −1.14918 |
OTU_516 | D_0__Bacteria | D_1__Proteobacteria | D_2__Alphaproteobacteria | D_3__Rickettsiales | D_4__Mitochondria | D_5__Triticum aestivum (bread wheat) | D_6__Triticum aestivum (bread wheat) | −0.13817 | −0.15863 | 0.151402 |
Step 2: Obtain the estimated standard errors of beta.
Step 3: Obtain the test statistics.
Step 4: Obtain the P-values from the two-sided Z-test using the test statistics.
Step 5: Obtain the Adjusted P-values by applying the p_adj_method() function.
The adjusted P-values of differentially abundant analysis of taxa in QtRNA microbiome data
Kingdom | Phylum | Class | Order | Family | Genus | Species | Group | TimePost | Group:TimePost | |
|---|---|---|---|---|---|---|---|---|---|---|
OTU_56 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus caecimuris B7 | 1 | 1 | 1 |
OTU_57 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus muris | 1 | 1 | 1 |
OTU_58 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__mouse gut metagenome | 1 | 0.012024 | 1 |
OTU_77 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Bacteroidaceae | D_5__Bacteroides | D_6__Bacteroides acidifaciens JCM 10556 | 0 | 1 | 0 |
OTU_101 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Muribaculaceae | D_5__Muribaculum | D_6__Parabacteroides sp. YL27 | 1 | 1 | 0.409359 |
OTU_131 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Tannerellaceae | D_5__Parabacteroides | D_6__Parabacteroides goldsteinii CL02T12C30 | 1 | 0.522427 | 1 |
OTU_231 | D_0__Bacteria | D_1__Deferribacteres | D_2__Deferribacteres | D_3__Deferribacterales | D_4__Deferribacteraceae | D_5__Mucispirillum | D_6__Mucispirillum schaedleri ASF457 | 1 | 1 | 1 |
OTU_263 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus saprophyticus subsp. saprophyticus | 1 | 0.54287 | 1 |
OTU_264 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus sp. UAsDu23 | 1 | 4.80E-06 | 1 |
OTU_276 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__Lactobacillus murinus | 0 | 1 | 0 |
OTU_279 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__gut metagenome | 1 | 1 | 1 |
OTU_287 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Streptococcaceae | D_5__Streptococcus | D_6__Streptococcus danieliae | 1 | 1 | 1 |
OTU_323 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__ASF356 | D_6__Clostridium sp. ASF356 | 0 | 1 | 0 |
OTU_325 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Acetatifactor | D_6__Clostridiales bacterium CIEAF 015 | 1 | 0.008759 | 1 |
OTU_330 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Anaerostipes | D_6__Clostridiales bacterium VE202-09 | 1 | 1 | 1 |
OTU_351 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Clostridiales bacterium CIEAF 020 | 1 | 1 | 1 |
OTU_353 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium A4 | 1 | 1 | 1 |
OTU_354 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium COE1 | 1 | 1 | 0.169092 |
OTU_361 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae UCG-006 | D_6__Clostridium sp. ASF502 | 1 | 1 | 1 |
OTU_366 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Marvinbryantia | D_6__Clostridiales bacterium CIEAF 012 | 1 | 1 | 1 |
OTU_369 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Clostridium sp. Clone-44 | 0 | 1 | 0 |
OTU_370 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Eubacterium sp. 14-2 | 1 | 0.00047 | 1 |
OTU_395 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Anaerotruncus | D_6__Anaerotruncus sp. G3(2012) | 1 | 0.000105 | 1 |
OTU_408 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Clostridium sp. Culture Jar-8 | 0 | 2.38E-47 | 0 |
OTU_409 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Ruminiclostridium sp. KB18 | 1 | 0.636737 | 1 |
OTU_412 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 9 | D_6__bacterium enrichment culture clone M244 | 0 | 1 | 0 |
OTU_516 | D_0__Bacteria | D_1__Proteobacteria | D_2__Alphaproteobacteria | D_3__Rickettsiales | D_4__Mitochondria | D_5__Triticum aestivum (bread wheat) | D_6__Triticum aestivum (bread wheat) | 0 | 1 | 0 |
Step 6: Identify the differentially abundant taxa (Table 14.6).
The identified differentially abundant taxa in QtRNA microbiome data
Kingdom | Phylum | Class | Order | Family | Genus | Species | Group | TimePost | Group:TimePost | |
|---|---|---|---|---|---|---|---|---|---|---|
OTU_56 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus caecimuris B7 | FALSE | FALSE | FALSE |
OTU_57 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__Enterorhabdus muris | FALSE | FALSE | FALSE |
OTU_58 | D_0__Bacteria | D_1__Actinobacteria | D_2__Coriobacteriia | D_3__Coriobacteriales | D_4__Eggerthellaceae | D_5__Enterorhabdus | D_6__mouse gut metagenome | FALSE | TRUE | FALSE |
OTU_77 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Bacteroidaceae | D_5__Bacteroides | D_6__Bacteroides acidifaciens JCM 10556 | TRUE | FALSE | TRUE |
OTU_101 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Muribaculaceae | D_5__Muribaculum | D_6__Parabacteroides sp. YL27 | FALSE | FALSE | FALSE |
OTU_131 | D_0__Bacteria | D_1__Bacteroidetes | D_2__Bacteroidia | D_3__Bacteroidales | D_4__Tannerellaceae | D_5__Parabacteroides | D_6__Parabacteroides goldsteinii CL02T12C30 | FALSE | FALSE | FALSE |
OTU_231 | D_0__Bacteria | D_1__Deferribacteres | D_2__Deferribacteres | D_3__Deferribacterales | D_4__Deferribacteraceae | D_5__Mucispirillum | D_6__Mucispirillum schaedleri ASF457 | FALSE | FALSE | FALSE |
OTU_263 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus saprophyticus subsp. saprophyticus | FALSE | FALSE | FALSE |
OTU_264 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Bacillales | D_4__Staphylococcaceae | D_5__Staphylococcus | D_6__Staphylococcus sp. UAsDu23 | FALSE | TRUE | FALSE |
OTU_276 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__Lactobacillus murinus | TRUE | FALSE | TRUE |
OTU_279 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Lactobacillaceae | D_5__Lactobacillus | D_6__gut metagenome | FALSE | FALSE | FALSE |
OTU_287 | D_0__Bacteria | D_1__Firmicutes | D_2__Bacilli | D_3__Lactobacillales | D_4__Streptococcaceae | D_5__Streptococcus | D_6__Streptococcus danieliae | FALSE | FALSE | FALSE |
OTU_323 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__ASF356 | D_6__Clostridium sp. ASF356 | TRUE | FALSE | TRUE |
OTU_325 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Acetatifactor | D_6__Clostridiales bacterium CIEAF 015 | FALSE | TRUE | FALSE |
OTU_330 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Anaerostipes | D_6__Clostridiales bacterium VE202-09 | FALSE | FALSE | FALSE |
OTU_351 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Clostridiales bacterium CIEAF 020 | FALSE | FALSE | FALSE |
OTU_353 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium A4 | FALSE | FALSE | FALSE |
OTU_354 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae NK4A136 group | D_6__Lachnospiraceae bacterium COE1 | FALSE | FALSE | FALSE |
OTU_361 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Lachnospiraceae UCG-006 | D_6__Clostridium sp. ASF502 | FALSE | FALSE | FALSE |
OTU_366 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Marvinbryantia | D_6__Clostridiales bacterium CIEAF 012 | FALSE | FALSE | FALSE |
OTU_369 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Clostridium sp. Clone-44 | TRUE | FALSE | TRUE |
OTU_370 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Lachnospiraceae | D_5__Roseburia | D_6__Eubacterium sp. 14-2 | FALSE | TRUE | FALSE |
OTU_395 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Anaerotruncus | D_6__Anaerotruncus sp. G3(2012) | FALSE | TRUE | FALSE |
OTU_408 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Clostridium sp. Culture Jar-8 | TRUE | TRUE | TRUE |
OTU_409 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 5 | D_6__Ruminiclostridium sp. KB18 | FALSE | FALSE | FALSE |
OTU_412 | D_0__Bacteria | D_1__Firmicutes | D_2__Clostridia | D_3__Clostridiales | D_4__Ruminococcaceae | D_5__Ruminiclostridium 9 | D_6__bacterium enrichment culture clone M244 | TRUE | FALSE | TRUE |
OTU_516 | D_0__Bacteria | D_1__Proteobacteria | D_2__Alphaproteobacteria | D_3__Rickettsiales | D_4__Mitochondria | D_5__Triticum aestivum (bread wheat) | D_6__Triticum aestivum (bread wheat) | TRUE | FALSE | TRUE |
Step 7: Estimate and adjust the sample-specific sampling fractions to obtain the bias-adjusted abundances.
First, estimate sample-specific sampling fractions by natural log scale. Since the sampling fraction is not estimable for each sample with the presence of missing values, the missing values (NA) for any variable specified in the formula will be replaced with 0.
Then, adjust the log observed abundances by subtracting the estimated sampling fraction from log observed abundances of each sample. Note that to avoid taking the log of 0, which is undefined, a pseudocount (here 1) is added to each estimated abundances before taking natural log.
ANCOMBC Global Test.
In the sample metadata, we created a four levels of categorical variable “Group4” (WT_BEFORE, WT_POST, KO_BEFORE, and KO_POST). We used the following commands to illustrate the ANCOM-BC global test using this variable.
The global test results are contained in the output$res_global (a data.frame for the variable specified in group).
Step 1: Obtain the test global statistics.
Step 2: Obtain the P-values from the two-sided Z-test using the global test statistics.
Step 3: Adjust the P-values by applying the p_adj_method() function for the global test.
Step 4: Identify the differentially abundant taxa for the global test.
14.4.3 Remarks on ANCOM-BC
- ANCOM-BC method has some unique characteristics (Lin and Peddada 2020a): (1) It explicitly tests hypothesis of differential absolute abundance of individual taxon and provides valid P-values and confidence intervals for each taxon. (2) It provides an approach to estimate the sampling fraction and performs DA analysis by correcting bias due to (unobservable) differential sampling fractions across samples. (3) It does not rely on strong parametric assumptions. ANCOM-BC has some strengths (Lin and Peddada 2020a):
It can construct confidence intervals for DA of each taxon whereas ANCOM and other DA methods cannot. For example, we can construct a 95% simultaneous confidence intervals using Bonferroni method for the mean DA of each taxon in the two experimental groups, and hence an effect size that is associated with each taxon can be obtained in comparing two experimental groups.
It was demonstrated that like ANCOM, ANCOM-BC is able to well control the FDR while maintaining adequate power compared to other often used DA methods, including count-based methods edgeR and DESeq2 in RNA-seq studies, the zero-inflated Gaussian mixture model used in metagenomeSeq (ZIG) (Lin and Peddada 2020a).
- ANCOM-BC also has some weaknesses, for example:
ANCOM-BC cannot well control the FDR for small sample sizes (e.g., n = 5 per group). Ten samples are required for controlling FDR with adequate power (Lin and Peddada 2020a). This is probably because the estimator and the test statistic of ANCOM-BC are developed asymptotically.
ANCOM-BC assumes that the compositional data on the covariates is linear. Like ANCOM, ANCOM-BC cannot control the FDR well when this linear assumption is violated (Wang 2021).
ANCOM-BC adopted the methodology (Kaul et al. 2017) for dealing structural zeros, the outlier zeros, and sampling zeros. In practice, ANCOM-BC actually drops taxa in the analysis when the structural zeros associated with these taxa are detected by the criteria (Kaul et al. 2017).
ANCOM-BC uses log-transformation of OTU counts data rather than log-ratio transformation, ANCOM-BC methodology is not a typical CoDa in the sense of Aitchison’s approach (Aitchison 1986a). To solve the problem of compositionality, ANCOM-BC uses the sum of ecosystem as reference to offset the data. This kind of normalization is not the typical Aitchison’s approach, while like using offset in the count-based methods.
ANCOM and ANCOM-BC share some common features: (1) assuming that the observed sample is an unknown fraction of a unit volume of the ecosystem, and the sampling fraction varies from sample to sample, and (2) using log-ratio transformation (or log scale) to serve as normalization.
Unlike ANCOM, ANCOM-BC does not directly implement a log-ratio transformation, instead simplifies DA analysis by recasting the problem as a linear regression problem with an offset to account for the sampling fraction. That is, ANCOM-BC’s bias correction is a sample-specific offset term that is introduced into a linear regression and accounts for sampling fraction in conjunction with performing linear regression in log scale serves the same purpose as a log-ratio transformation.
Compared to ANCOM, ANCOM-BC is very fast because it avoids repeatedly using a taxon as reference that ANCOM uses. ANCOM needs
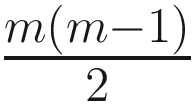 linear regressions to fit the models, whereas ANCOM-BC requires only m linear regressions to fit.
linear regressions to fit the models, whereas ANCOM-BC requires only m linear regressions to fit.
14.5 Remarks on Compositional Data Analysis Approach
In microbiome study, two kinds of statistical methods are available: count-based approach and compositional data analysis (CoDa) approach. The count-based approach, i.e., negative binomial methods (e.g., edgeR and DESeq2), and over-dispersed and zero-inflated models (e.g., metagenomeSeq) do not take data transformations to bring the data to normality before analysis, instead of using the offset to scale the data during the modeling.
Different from count-based approach, CoDa approach including ALDEx2, ANCOM, and ANCOM-BC typically need some kind of log or log-ratio transformations before analysis.
In some instances, the log-ratio transformation is technically equivalent to a normalization such as alr- and clr-transformations can formally serve as effective library size normalizations. Thus sometime the log-ratio transformation is called the log-ratio “normalization” (Quinn et al. 2018a, b). The parametric methods (ALDEx2 t-test, ANCOM-BC) in CoDa approach further assume a Gaussian distribution of the data in their statistical models. Since it is difficult to measure total microbial load or absolute number of microorganisms to accurately determine taxonomic shifts (Morton et al. 2019), there remains a lack of a gold standard to measure microbiome data. Thus, DA analysis is still controversial in microbiome research. One current effort tries to establish microbial composition measurement standards with reference frames and define the concept of “reference frames” for inferring changes in abundance in CoDa. The “reference frames” are used as a constraint for inferencing how microbial populations change relatively given by other microbial populations. The reference frame for inferring changes is determined by denominator in a log-ratio (Morton et al. 2019).
CoDa methods have their advantages, providing a statistical tool to move from the simplex into real space (Aitchison et al. 2000) and hence enable statistical methods in Euclidean distances. Thus, log-ratio “normalizations” or log-ratio transformations are useful even when they do not normalize the data. As we reviewed in this chapter, ALDEx2, ANCOM, and ANCOM-BC methods have been evaluated and compared to edgeR, DESeq2, metagenomeSeq, and other competing methods. Their robustness and privileges are claimed by the proposed authors.
However, we notice that when ANCOM-BC claimed that both ANCOM and ANCOM-BC are outperformed over edgeR, and DESeq2, and ZIG in terms of FDR control and higher power, their DA analyses in concept are different. For example, ANCOM-BC differentially analyzes absolute abundance rather than differentially analyzes relative abundance. When ANCOM-BC states that it takes into account the compositionality of the microbiome data, it actually uses log-transformation to transform the OTU data or use an offset to account for the sampling fraction. Additionally, both edgeR and DESeq2 were developed based on NB models to account for small sample sizes and individual variation of genes (taxa). Overall, the concept and approach of reference frames remain within the CoDa with log-ratio transformation. Thus, it still has the challenge to deal with zero-problem and in practice how to pick an appropriate reference frame and to understand statistical properties of these reference frames (Morton et al. 2019). We should consider the context when we explain the performance of model comparisons.
However, on the one hand, whether or not microbiome data are really compositional is debatable. Some researchers acknowledged that next-generation sequencing (NGS) abundance data differ slightly from the formally defined compositional data because they contain integer values only, such as NGS abundance data do not require the arbitrary sum to represent complete unity in Aitchison’s definition of compositional data (Aitchison 1982, 1986a). Thus, many datasets such as possibly NGS abundance data lack the information of potential components and hence exist as “incomplete compositions” (Quinn et al. 2018a, b). But this kind of data (e.g., NGS abundance data) is incidentally constrained to an arbitrary sum, and thus it still has compositional properties and can be called “count compositional data” and treated as compositional data (Lovell et al. 2015; Quinn et al. 2017, 2018a, b). In contrast, other researchers do not think that count data is purely relative—the count pair (1, 2) carries different information than counts of (1000, 2000) even though the ratio of the two pair is same. Instead, they think that treating count data as compositional is treating “really discrete count data” as continuous (Bacon-Shone 2008).
- (1)
Compositionality (e.g., the spurious correlation concern) occurs when the data dimension is relatively low (i.e., the number of components is relatively small), such as in ecology studies. However, microbiome data is high dimensional and usually having the large number of taxa. Even there is the compositional effect (e.g., the spurious correlation), its effect is mild when the samples have large diversity (Zhang et al. 2017; Friedman and Alm 2012) because as the number of taxa increases, the compositional effect is attenuating (Hu et al. 2018).
- (2)
The mild data compositionality can be corrected by technological developments including the estimation of absolute cellular abundances from microbiome sequence data in microbiome data science (Vandeputte et al. 2017).
- (3)
The count-based models do not require the data to be transformed before analysis. It was shown these models have more statistical power to detect differential expression (Robinson and Oshlack 2010; Zhang and Yi 2020). Thus, these researchers advised to treat the high-throughput sequencing datasets as count data (Anders et al. 2013; Kuczynski et al. 2011).
- (4)
Compositional data analysis may lack strong biological interpretation. The results from transformation-based analyses should be interpreted with respect to the chosen reference or the results should be translated back into compositional terms. This remains complicated. Otherwise it is difficult to interpret biologically because one purpose of microbiome study is to detect which taxa are associated with the outcome (Hu et al. 2018) rather than to detect the association between ratio of taxa and the outcome. Thus, CoDa uses the ratio of taxa to interpret the results have been criticized because of no clinical-direct-relevance (Xia 2020).
- (5)
Compositional data analysis usually takes log-ratio transformation to transform the abundance count data before analysis. To ensure log of zeros be defined, arbitrary small constant counts are added to a zero value. Thus, how best to handle zeros remains a topic of ongoing research and poses the major challenge of CoDa (Xia 2020).
Both compositional and count-based models are based on abundance read counts. Actually, functional study indicates that the rare taxa with lower abundant read counts do not necessarily have lower functions related to the health and disease. Thus, the statistical models that are sensitive to detect these rare taxa are especially important.
14.6 Summary
This chapter focused on principles, methods, and techniques of compositional data analysis in microbiome data. First, we described overall compositional data analysis (CoDa) including definition of compositional data, description of the reasons that some researchers treat microbiome data as compositional, definition of Aitchison simplex, description of the challenges of analyzing compositional data, fundamental principles of CoDa, and the family of log-ratio transformations: additive log-ratio (alr), centered log-ratio (clr), isometric log-ratio (ilr), and inter-quartile log-ratio (iqlr). Next, we introduced and illustrated three CoDa, respectively, in the order of these methods proposed: (1) ANOVA-Like Compositional Differential Abundance Analysis (ALDEx2), (2) Analysis of Composition of Microbiomes (ANCOM), and (3) Analysis of Composition of Microbiomes-Bias Correction (ANCOM-BC). We implemented ALDEx2 and ANCOM-BC with R and ANCOM using QIIME 2. We also provided some general remarks on the approach of CoDa.
In Chap. 15, we will introduce how to analyze longitudinal microbiome data through linear mixed-effects models.